📘 What is a Confusion Matrix?

Imagine you teach a computer to tell the difference between dogs and cats. To know if the computer is learning well, you check its answers against the real answers.

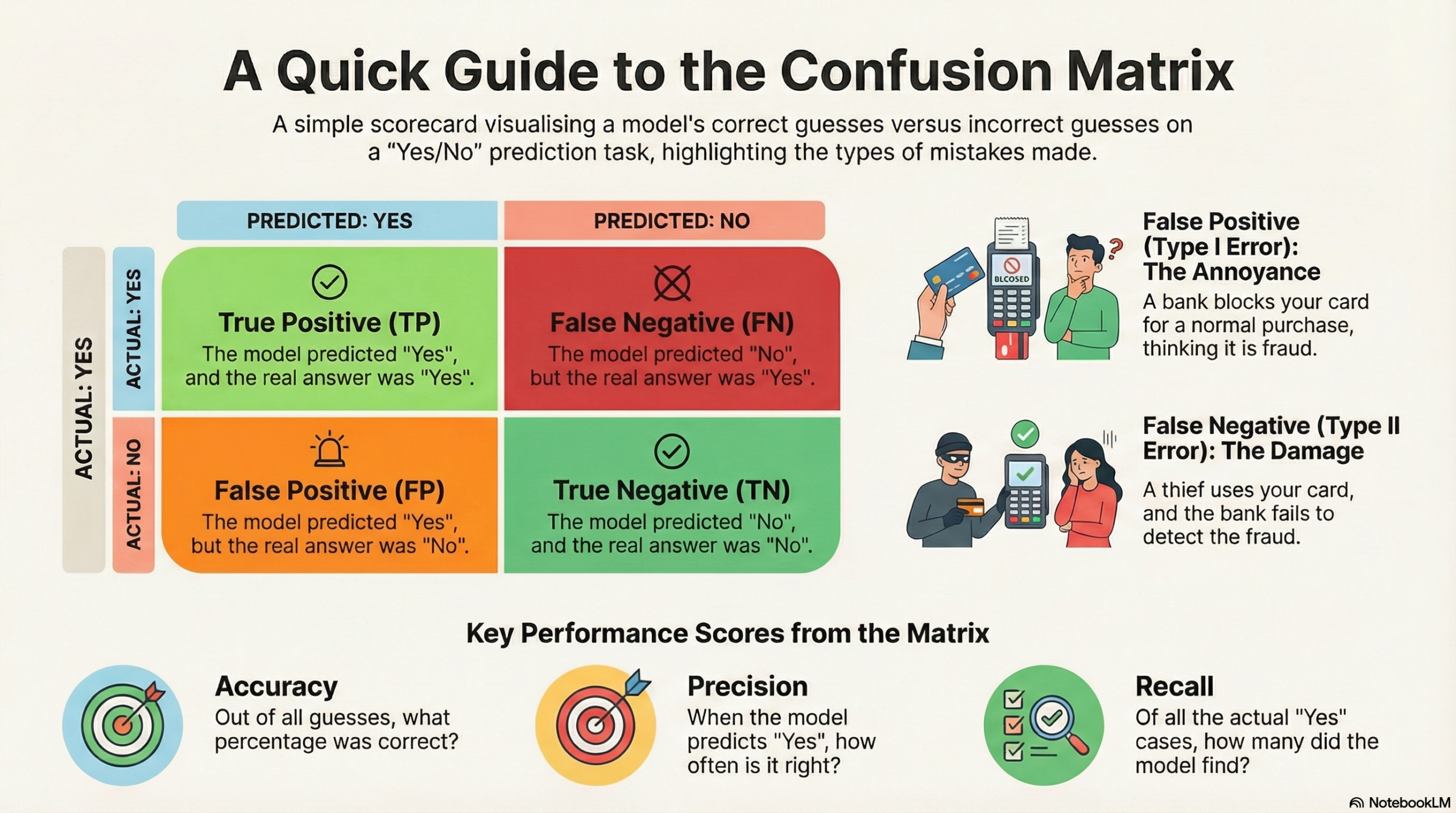
A Confusion Matrix is just a table (a scorecard) that shows us:

1. When the computer was Right.
2. When the computer was Wrong.
3. How it was wrong (what kind of mistake it made).

We usually use this for “Yes/No” problems (like: Is it Fraud? Is it Spam? Is it Sick?).

Confusion Matrix

🟢 The 4 Key Outcomes

There are only 4 possible things that can happen when the computer makes a guess. We use the terms Positive (Yes, it is fraud) and Negative (No, it is safe).

Term	What it means (Simple English)	Example in Fraud Detection
TP (True Positive)	The computer guessed Yes, and the real answer was Yes.	Computer said “Fraud” and it really was fraud. ✅
TN (True Negative)	The computer guessed No, and the real answer was No.	Computer said “Safe” and it really was safe. ✅
FP (False Positive)	The computer guessed Yes, but the real answer was No.	Computer said “Fraud” but it was actually a safe buy. ❌
FN (False Negative)	The computer guessed No, but the real answer was Yes.	Computer said “Safe” but it was actually fraud. ❌

📊 The Matrix Table

Here is how we arrange those numbers into a grid.

• Rows = The Real Truth (Actual).
• Columns = The Computer’s Guess (Predicted).

	Computer Guesses: YES	Computer Guesses: NO
Real Truth is: YES	TP (Correct)	FN (Missed it)
Real Truth is: NO	FP (False Alarm)	TN (Correct)

🔍 Types of Errors

In simple statistics, we give names to the mistakes:

1. FP = Type I Error (False Alarm)

• Meaning: The alarm rings when there is no fire.
• Example: You try to buy a pizza, but the bank blocks your card thinking it is fraud.
• Result: Annoying, but you can usually fix it by calling the bank.

2. FN = Type II Error (The Dangerous Miss)

• Meaning: The alarm stays silent when there is a fire.
• Example: A thief steals your credit card info and buys a laptop, but the bank thinks it is you.
• Result: You lose money. This is usually more dangerous than a False Alarm.

💡 Real-Life Example: The Email Spam Filter

Let’s say you have an email filter that tries to block spam emails.

• Positive (+) = Spam Email.
• Negative (-) = Good Email (from friends/boss).

Outcome	Meaning	Is it bad?
TP	Filter puts a spam email in the junk folder.	✅ Good!
TN	Filter lets a good email go to your inbox.	✅ Good!
FP	Filter puts a good email from your boss in the junk folder.	❌ Bad! You might miss an important meeting.
FN	Filter lets a spam email into your inbox.	❌ Bad! You get annoying scam messages.

📈 Important Metrics (The Score)

The matrix gives us the numbers, but we often use those numbers to calculate grades for the computer.

1. Accuracy: Out of all guesses, how many were right?
   • Formula: (TP+TN)/Total 2. Precision: When the computer says “Yes”, how often is it actually right? (How many alarms were real fires?)
   • Formula: TP/(TP+FP) 3. Recall (Sensitivity): Out of all the real “Yes” events, how many did the computer catch? (Did it catch all the fraud?)
   • Formula: TP/(TP+FN)

💻 Understanding the Python Code

You provided code in your prompt. Here is a simple explanation of what that code is doing, step-by-step:

1. make_classification: This creates fake data for us to practice with. It creates 1000 rows of data with 2 categories (Class 0 and Class 1).
2. train_test_split: We cut the data into two piles.
   • Train pile: To teach the computer.
   • Test pile: To test the computer later (like a final exam).
3. LogisticRegression: This is the “Brain” (Model) we are teaching.
4. model.fit: The computer studies the Train pile.
5. model.predict: The computer guesses the answers for the Test pile.
6. confusion_matrix: This compares the computer’s guesses (y_pred) against the real answers (y_test) and gives us the table of TP, TN, FP, FN.
7. ConfusionMatrixDisplay: This draws the colorful picture so you can see the results easily.

Confusion Matrix

💻 Python Code (Fraud Detection with Confusion Matrix)

This code trains a Logistic Regression model and prints the raw confusion matrix numbers before showing the visual chart.

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
import matplotlib.pyplot as plt

# 1. Generate sample data (1000 fake transactions)
X, y = make_classification(n_samples=1000, n_features=5, n_classes=2, random_state=42)

# 2. Split data: 80% training, 20% testing
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

# 3. Train Logistic Regression model
model = LogisticRegression()
model.fit(X_train, y_train)

# 4. Predict test data
y_pred = model.predict(X_test)

# 5. Create confusion matrix
cm = confusion_matrix(y_test, y_pred)

# Print raw values
print("Confusion Matrix (Raw Numbers):")
print(cm)
print("\nMapping of the matrix:")
print("[[TN, FP],")
print(" [FN, TP]]")

# 6. Plot confusion matrix
disp = ConfusionMatrixDisplay(
    confusion_matrix=cm,
    display_labels=['Not Fraud (0)', 'Fraud (1)']
)

disp.plot(cmap='Blues')
plt.title('Confusion Matrix: Fraud Detection')
plt.show()

🖥️ Output of the Code

1️⃣ Console Output (Raw Numbers)

Confusion Matrix (Raw Numbers):
[[96  4]
 [ 6 94]]

Mapping of the matrix:
[[TN, FP],
 [FN, TP]]

2️⃣ Visual Output (Confusion Matrix Chart)

Actual \ Predicted	Not Fraud	Fraud
Not Fraud	96 (Dark Blue)	4 (Light Blue)
Fraud	6 (Light Blue)	94 (Dark Blue)

📌 Darker blue = higher value

🧐 How to Read the Confusion Matrix

🔹 Row 1: Actual = Not Fraud (0)

• 96 → TN (True Negative)
  Correctly identified safe transactions ✅
• 4 → FP (False Positive)
  Safe transactions wrongly flagged as fraud ❌
  👉 Type I Error

🔹 Row 2: Actual = Fraud (1)

• 6 → FN (False Negative)
  Fraud transactions missed by the system ❌
  👉 Type II Error (Most Dangerous)
• 94 → TP (True Positive)
  Fraud correctly detected ✅

🚨 Error Summary

Error Type	Value	Meaning
Type I Error (FP)	4	False alarm
Type II Error (FN)	6	Missed fraud

🎯 Final Takeaway (Exam-Ready)

In fraud detection, False Negatives (Type II errors) are more dangerous than False Positives (Type I errors).
Therefore, models are often tuned to catch more fraud, even if it causes a few false alarms.

Confusion Matrix

About the Author

Aryugyan

Administrator

Visit Website View All Posts