What is Naive Bayes?

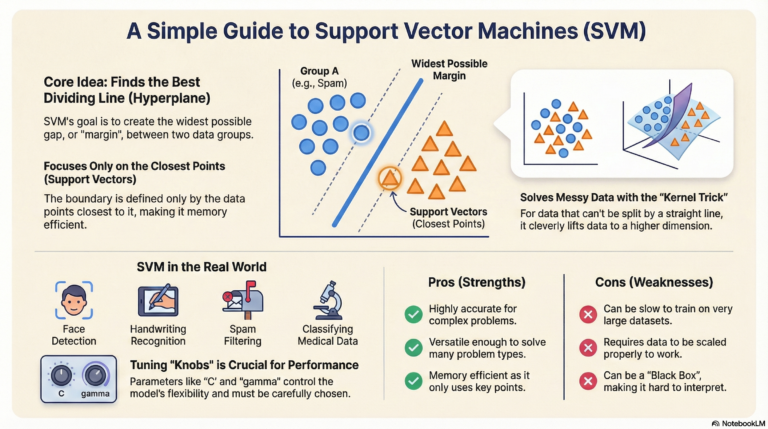
Naive Bayes is a classification algorithm based on Bayes’ Theorem and the assumption of feature independence.

It’s called “naive” because it assumes that all features are independent of each other — which is rarely true in real life — but still works well for many classification problems like spam detection, sentiment analysis, and document categorization.

---

📚 Bayes’ Theorem (Supervised)

Bayes’ Theorem helps us calculate the probability of an event occurring given prior knowledge.

Where:

• P(A∣B): Probability of A given B (Posterior)
• P(B∣A): Probability of B given A (Likelihood)
• P(A): Probability of A (Prior)
• P(B): Probability of B (Evidence)

Where:

• P(Class): Probability of the class (prior)
• P(Features∣Class): Likelihood
• P(Features): Evidence (constant for all classes)
• P(Class∣Features): Posterior (what we want to compute)

Since P(Features) is the same for all classes, we can ignore it and compare only:P(Class∣Features)∝P(Features∣Class)⋅P(Class)

🧪 Types of Naive Bayes Models

1. Gaussian Naive Bayes : Assumes continuous values follow a normal distribution.
2. Multinomial Naive Bayes : Used for discrete counts (e.g., word frequencies in text).
3. Bernoulli Naive Bayes : Used for binary/boolean features (yes/no).

We’ll use Multinomial Naive Bayes in our example.

---

🎯 Problem Example: Play Tennis or Not?

Let’s take a small dataset where we want to predict whether someone will play tennis based on weather conditions.

Outlook	Temperature	Humidity	Wind	Play
Sunny	Hot	High	Weak	No
Sunny	Hot	High	Strong	No
Overcast	Hot	High	Weak	Yes
Rain	Mild	High	Weak	Yes
Rain	Cool	Normal	Weak	Yes
Rain	Cool	Normal	Strong	No
Overcast	Cool	Normal	Strong	Yes
Sunny	Mild	High	Weak	No
Sunny	Cool	Normal	Weak	Yes
Rain	Mild	Normal	Weak	Yes
Sunny	Mild	Normal	Strong	Yes
Overcast	Mild	High	Strong	Yes
Overcast	Hot	Normal	Weak	Yes
Rain	Mild	High	Strong	No

Our goal: Predict if they will Play based on weather features.

🔢 Step-by-Step Manual Calculation

Step 1: Count how many times each class appears

Total rows = 14

• Yes (Play) = 9 times
• No (Don’t Play) = 5 times

So:

• P(Yes)=9/14≈0.64
• P(No)=5/14≈0.36

Step 2: Calculate probabilities for each feature per class

Let’s say we want to predict:

Will they play if the outlook is Sunny , temperature is Cool , humidity is Normal , and wind is Strong ?

a technique called Laplace Smoothing (also known as Additive Smoothing )

Where:

• count(xi in Ck) = how many times that feature value appears in class Ck
• count(Ck) = total number of instances in class Ck
• N = number of unique possible values for that feature(Sunny,Overcast,Rain)

📌 General Rule: Use Laplace Smoothing for Each Feature Separately

Each feature has its own number of categories. For example:

Feature	Unique Values	Value of N
Outlook	Sunny, Overcast, Rain	3
Temperature	Hot, Mild, Cool	3
Humidity	High, Normal	2
Wind	Weak, Strong	2

For class Yes :

Count how often each feature occurs when Play = Yes.

Feature	Count when Yes	Total Yes = 9	Probability (with smoothing)
Outlook=Sunny	2	9	(2 + 1)/(9 + 3) = 3/12 ≈ 0.25
Temp=Cool	3	9	(3 + 1)/12 ≈ 0.33
Humidity=Normal	4	9	(4 + 1)/12 ≈ 0.42
Wind=Strong	2	9	(2 + 1)/12 ≈ 0.25

Add 1 to numerator and number of categories to denominator for Laplace smoothing .

Multiply all together and multiply by P(Yes):

P(Yes∣X)=P(Sunny∣Yes)⋅P(Cool∣Yes)⋅P(Normal∣Yes)⋅P(Strong∣Yes)⋅P(Yes∣X)=0.25×0.33×0.42×0.25×0.64≈0.0055

Do same for class No :

Feature	Count when No	Total No = 5	Probability (with smoothing)
Outlook=Sunny	3	5	(3 + 1)/(5 + 3) = 4/8 = 0.5
Temp=Cool	1	5	(1 + 1)/8 = 0.25
Humidity=Normal	1	5	(1 + 1)/8 = 0.25
Wind=Strong	2	5	(2 + 1)/8 = 0.375

P(No∣X)=0.5×0.25×0.25×0.375×0.36≈0.0042

---

Step 3: Compare Both Probabilities

• P(Yes∣X)=0.0055
• P(No∣X)=0.0042

Since 0.0055 > 0.0042 , we predict Yes → They will play tennis!

---

🧑‍💻 Summary of Naive Bayes Steps:

1. Calculate prior probabilities (P(Yes), P(No)).
2. For each feature , count how often it appears in each class.
3. Use Laplace smoothing to avoid zero probabilities.
4. Multiply all conditional probabilities and multiply by prior.
5. Choose class with highest probability as prediction.

---

✅ Advantages of Naive Bayes

• Simple and fast
• Works well with high-dimensional data (like text)
• Handles both numerical and categorical data

❌ Disadvantages

• Assumes all features are independent (not always true)
• Can give poor results if this assumption is violated

---

📝 Real-Life Uses

• Spam filtering
• Sentiment analysis
• Document categorization
• Medical diagnosis

---

📘 Final Notes

• Don’t worry too much about the math at first — focus on understanding the idea.
• Naive Bayes is great for beginners because it’s easy to implement and understand.
• You can try it using Python libraries like scikit-learn .

🧩 Optional: Python Code Example

from sklearn.naive_bayes import MultinomialNB
from sklearn.feature_extraction.text import CountVectorizer

# Sample data
X_train = [
    "sunny hot high weak",
    "sunny hot high strong",
    "overcast hot high weak",
    "rain mild high weak",
    "rain cool normal weak",
    "rain cool normal strong",
    "overcast cool normal strong",
    "sunny mild high weak",
    "sunny cool normal weak",
    "rain mild normal weak",
    "sunny mild normal strong",
    "overcast mild high strong",
    "overcast hot normal weak",
    "rain mild high strong"
]
y_train = ["No", "No", "Yes", "Yes", "Yes", "No", "Yes", "No", "Yes", "Yes", "Yes", "Yes", "Yes", "No"]

# Vectorize input
vectorizer = CountVectorizer()
X_vec = vectorizer.fit_transform(X_train)

# Train model
model = MultinomialNB()
model.fit(X_vec, y_train)

# Predict new instance
new_instance = ["sunny cool normal strong"]
new_vec = vectorizer.transform(new_instance)
prediction = model.predict(new_vec)

print("Prediction:", prediction[0])

output
Prediction: Yes