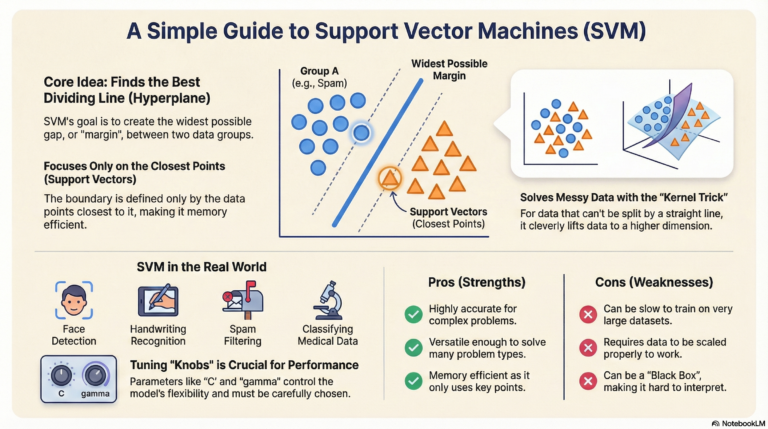
Unsupervised Learning
What is Unsupervised Learning?
Unsupervised learning is a machine learning approach in which algorithms learn patterns and structures from unlabeled data—data that contains only input features (X) without corresponding output labels.
The objective is not to predict predefined outcomes, but to discover hidden patterns, relationships, or groupings within the data. Since there are no correct answers provided, the model must infer meaningful structure on its own.
Unlike supervised learning, unsupervised learning has no “teacher” or ground truth labels, making it particularly useful for exploratory data analysis and insight generation.
How Unsupervised Learning Works
- Data Collection
Gather an unlabeled dataset containing only input features. - Pattern Discovery
The algorithm analyzes the data to identify inherent structures such as clusters, similarities, or associations. - Model Creation
A model is formed that represents the discovered patterns or relationships. - Insight Extraction
The results are used to gain insights into data organization, trends, or anomalies.
Types of Unsupervised Learning
1. Clustering
Clustering algorithms group similar data points together based on feature similarity.
- Creates clusters where items within the same group are more similar to each other than to those in other groups
- Examples:
- Customer segmentation
- Image segmentation
- Document grouping
2. Dimensionality Reduction
Dimensionality reduction techniques reduce the number of features while preserving the most important information.
- Makes high-dimensional data easier to analyze and visualize
- Improves computational efficiency
- Examples:
- Principal Component Analysis (PCA)
- t-SNE for visualization
3. Association Rule Mining
Association rule mining identifies interesting relationships and patterns among variables in large datasets.
- Discovers frequent item sets and correlations
- Commonly used in recommendation systems
- Examples:
- Market basket analysis
- Product recommendations
Key Characteristics of Unsupervised Learning
- No labeled data required
Works directly with raw, unlabeled datasets. - Discovers hidden patterns
Reveals relationships that may not be obvious through manual analysis. - Exploratory in nature
Commonly used for data understanding and hypothesis generation. - No ground truth supervision
There are no predefined correct answers. - Insight-focused
Emphasizes understanding data structure rather than making predictions.
Common Unsupervised Learning Algorithms
Clustering Algorithms
- K-Means Clustering
- Hierarchical Clustering
- DBSCAN (Density-Based Spatial Clustering of Applications with Noise)
- Gaussian Mixture Models (GMM)
- Mean-Shift Clustering
Dimensionality Reduction Techniques
- Principal Component Analysis (PCA)
- t-Distributed Stochastic Neighbor Embedding (t-SNE)
- Uniform Manifold Approximation and Projection (UMAP)
- Linear Discriminant Analysis (LDA)*
*Note: LDA is often considered supervised but is sometimes used in dimensionality reduction contexts.
Association Rule Mining Algorithms
- Apriori Algorithm
- Eclat Algorithm
- FP-Growth Algorithm
Code Examples
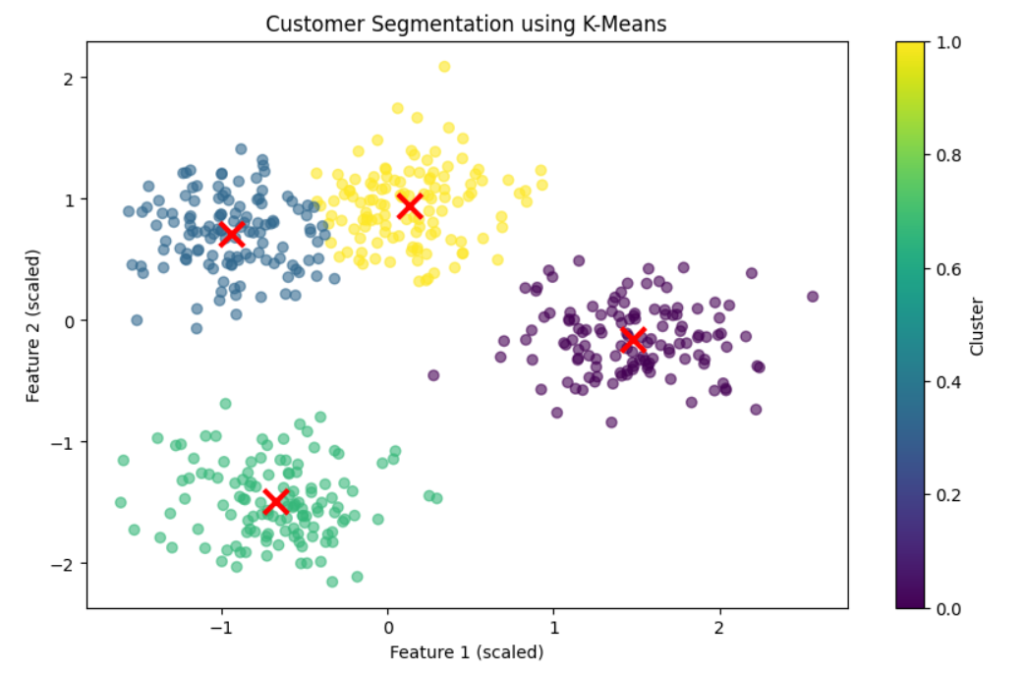
Example 1: K-Means Clustering for Customer Segmentation
In this example, we apply K-Means clustering to group customers based on feature similarity. This technique is widely used in marketing for customer segmentation.
Steps:
- Generate synthetic customer data
- Standardize the features
- Apply K-Means clustering
- Visualize clusters and centroids
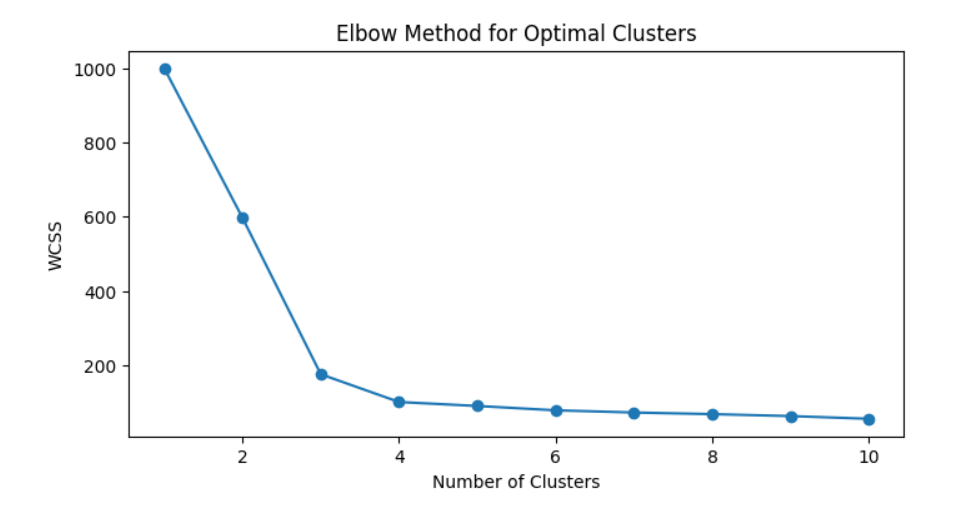
- Use the Elbow Method to find the optimal number of clusters
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_blobs
# Generate synthetic customer data
X, _ = make_blobs(
n_samples=500,
centers=4,
cluster_std=2.0,
random_state=42
)
# Standardize the data
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# Apply K-Means clustering
kmeans = KMeans(n_clusters=4, random_state=42)
kmeans.fit(X_scaled)
labels = kmeans.labels_
centroids = kmeans.cluster_centers_
# Visualize clusters
plt.figure(figsize=(10, 6))
plt.scatter(
X_scaled[:, 0],
X_scaled[:, 1],
c=labels,
cmap='viridis',
alpha=0.6
)
plt.scatter(
centroids[:, 0],
centroids[:, 1],
c='red',
marker='x',
s=200,
linewidths=3
)
plt.title("Customer Segmentation using K-Means")
plt.xlabel("Feature 1 (scaled)")
plt.ylabel("Feature 2 (scaled)")
plt.colorbar(label="Cluster")
plt.show()
# Elbow Method
wcss = []
for i in range(1, 11):
kmeans = KMeans(n_clusters=i, random_state=42)
kmeans.fit(X_scaled)
wcss.append(kmeans.inertia_)
plt.figure(figsize=(8, 4))
plt.plot(range(1, 11), wcss, marker='o')
plt.title("Elbow Method for Optimal Clusters")
plt.xlabel("Number of Clusters")
plt.ylabel("WCSS")
plt.show()
📌 Use Case: Customer segmentation, market analysis.
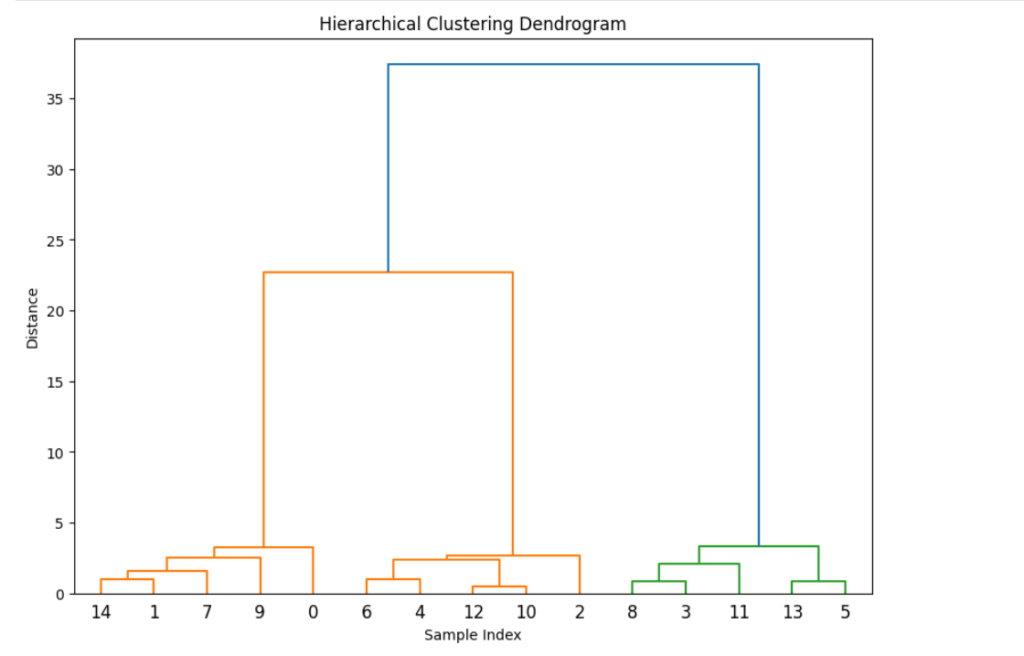
Example 2: Hierarchical Clustering with Dendrogram
Hierarchical clustering builds a tree-like structure (dendrogram) to visualize relationships between data points without specifying the number of clusters in advance.
Steps:
- Generate sample data
- Perform hierarchical clustering using Ward’s method
- Visualize the dendrogram
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import dendrogram, linkage
from sklearn.datasets import make_blobs
# Generate sample data
X, _ = make_blobs(n_samples=15, centers=3, random_state=42)
# Perform hierarchical clustering
linked = linkage(X, method='ward')
# Plot dendrogram
plt.figure(figsize=(10, 7))
dendrogram(
linked,
orientation='top',
distance_sort='descending',
show_leaf_counts=True
)
plt.title("Hierarchical Clustering Dendrogram")
plt.xlabel("Sample Index")
plt.ylabel("Distance")
plt.show()
📌 Use Case: Document clustering, genetic analysis.
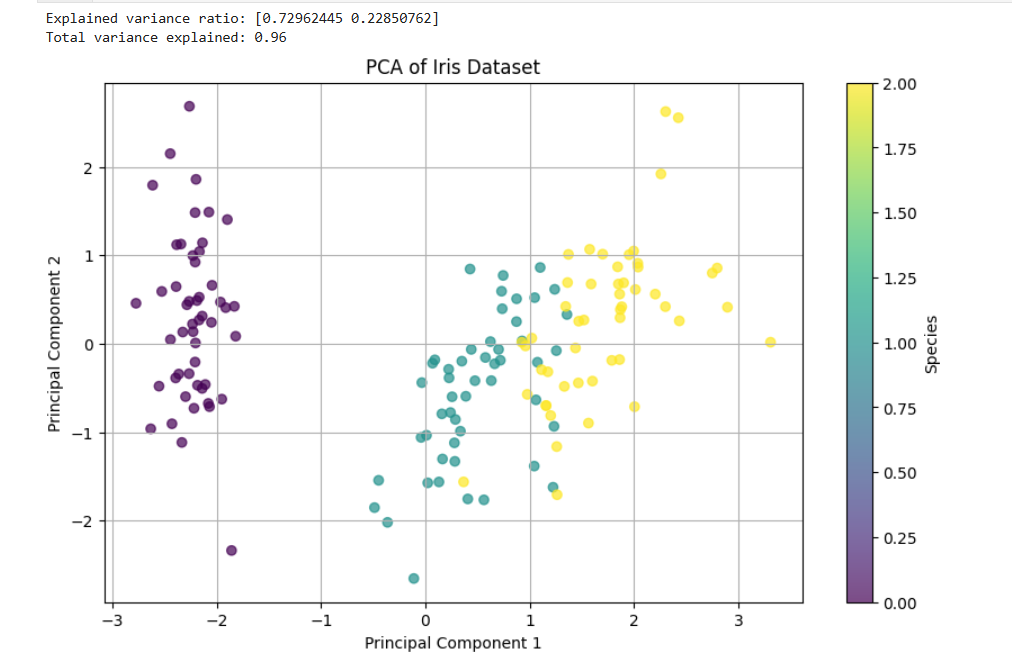
Example 3: PCA for Dimensionality Reduction
Principal Component Analysis (PCA) reduces high-dimensional data into fewer dimensions while preserving as much variance as possible. It is widely used for visualization and noise reduction.
Steps:
- Load the Iris dataset
- Standardize the features
- Apply PCA to reduce dimensions
- Visualize the transformed data
- Analyze explained variance
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
# Load dataset
iris = load_iris()
X = iris.data
y = iris.target
# Standardize the data
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# Apply PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)
# Visualization
plt.figure(figsize=(10, 6))
scatter = plt.scatter(
X_pca[:, 0],
X_pca[:, 1],
c=y,
cmap='viridis',
alpha=0.7
)
plt.title("PCA of Iris Dataset")
plt.xlabel("Principal Component 1")
plt.ylabel("Principal Component 2")
plt.colorbar(scatter, label="Species")
plt.grid(True)
# Explained variance
print("Explained variance ratio:", pca.explained_variance_ratio_)
print("Total variance explained:", round(sum(pca.explained_variance_ratio_), 2))
plt.show()
📌 Use Case: Data visualization, feature reduction, noise removal.
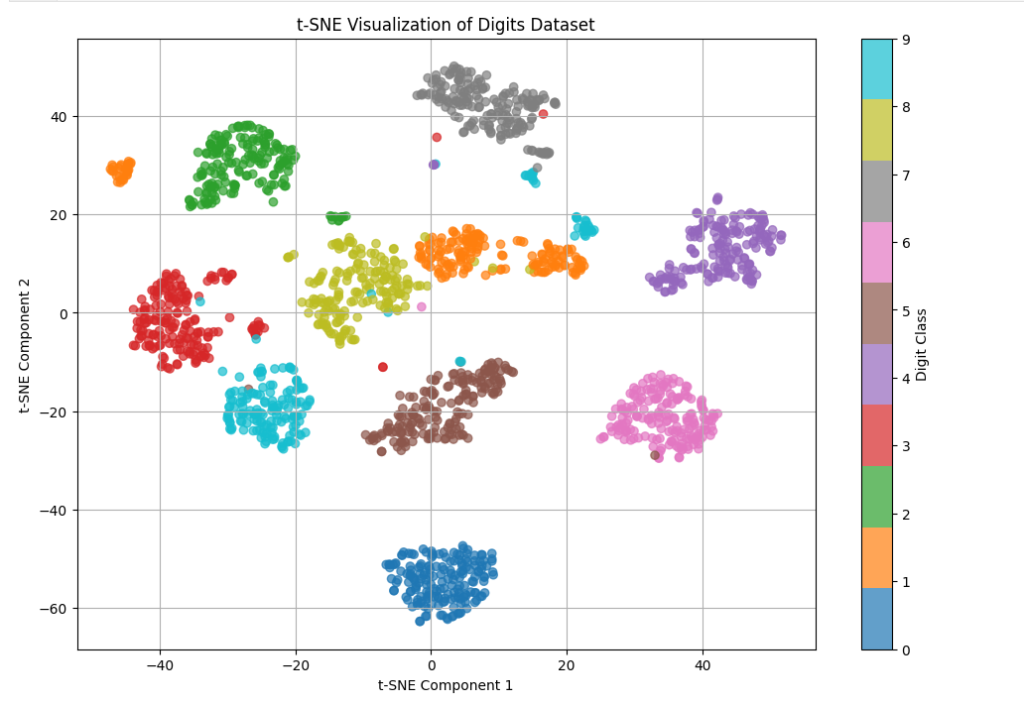
Example 4: t-SNE for Data Visualization
t-Distributed Stochastic Neighbor Embedding (t-SNE) is a non-linear dimensionality reduction technique ideal for visualizing complex, high-dimensional data.
Steps:
- Load handwritten digit data
- Apply t-SNE for 2D embedding
- Visualize clusters
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
from sklearn.datasets import load_digits
# Load dataset
digits = load_digits()
X = digits.data
y = digits.target
# Apply t-SNE
tsne = TSNE(
n_components=2,
random_state=42,
perplexity=30
)
X_tsne = tsne.fit_transform(X)
# Visualization
plt.figure(figsize=(12, 8))
scatter = plt.scatter(
X_tsne[:, 0],
X_tsne[:, 1],
c=y,
cmap='tab10',
alpha=0.7
)
plt.title("t-SNE Visualization of Digits Dataset")
plt.xlabel("t-SNE Component 1")
plt.ylabel("t-SNE Component 2")
plt.colorbar(scatter, label="Digit Class")
plt.grid(True)
plt.show()
📌 Use Case: Image data visualization, deep learning feature analysis.
⚠️ Note: t-SNE is computationally expensive and mainly used for visualization—not modeling.
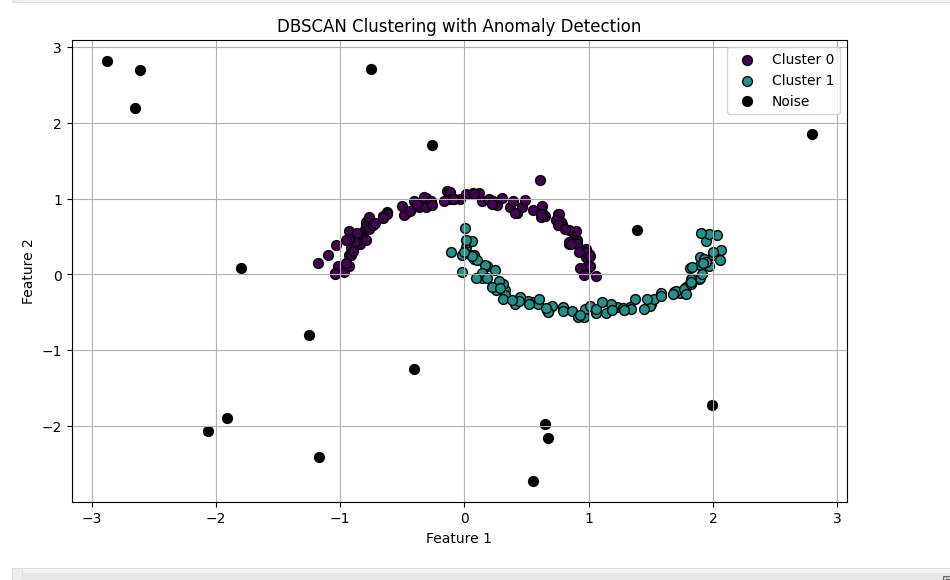
Example 5: DBSCAN for Anomaly Detection
DBSCAN (Density-Based Spatial Clustering of Applications with Noise) groups dense regions and identifies outliers automatically.
Steps:
- Generate moon-shaped data
- Add artificial outliers
- Apply DBSCAN
- Detect noise points
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import DBSCAN
from sklearn.datasets import make_moons
# Generate data
X, _ = make_moons(n_samples=200, noise=0.05, random_state=42)
# Add outliers
np.random.seed(42)
outliers = np.random.uniform(-3, 3, size=(20, 2))
X = np.vstack([X, outliers])
# Apply DBSCAN
dbscan = DBSCAN(eps=0.3, min_samples=5)
labels = dbscan.fit_predict(X)
# Visualization
plt.figure(figsize=(10, 6))
unique_labels = set(labels)
colors = plt.cm.viridis(np.linspace(0, 1, len(unique_labels)))
for label, color in zip(unique_labels, colors):
if label == -1:
color = 'black' # Noise points
label_name = "Noise"
else:
label_name = f"Cluster {label}"
mask = labels == label
plt.scatter(
X[mask, 0],
X[mask, 1],
c=[color],
label=label_name,
edgecolors='k',
s=50
)
plt.title("DBSCAN Clustering with Anomaly Detection")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.legend()
plt.grid(True)
plt.show()
📌 Use Case: Fraud detection, intrusion detection, outlier identification.
Summary Table
| Technique | Purpose | Strength |
|---|---|---|
| K-Means | Clustering | Fast, simple |
| Hierarchical | Clustering | Dendrogram visualization |
| PCA | Dimensionality Reduction | Preserves variance |
| t-SNE | Visualization | Captures non-linear patterns |
| DBSCAN | Clustering & Anomaly Detection | Detects noise |
Unsupervised Learning – Real-World Examples
1. Customer Segmentation in Marketing
Input:
- Customer purchase history
- Demographics
- Browsing behavior
Output:
- Customer segments (e.g., high-value customers, loyal customers, bargain hunters)
Algorithms:
- K-Means
- Hierarchical Clustering
Use Cases:
- Targeted marketing campaigns
- Personalized product recommendations
2. Document Clustering in Text Mining
Input:
- Text documents, articles, emails
Output:
- Topic clusters (sports, politics, technology, business, etc.)
Algorithms:
- K-Means
- Hierarchical Clustering with TF-IDF features
Use Cases:
- News content categorization
- Document management systems
- Email grouping
3. Anomaly Detection in Cybersecurity
Input:
- Network traffic data
- System logs
- User behavior patterns
Output:
- Normal behavior vs anomalous behavior
Algorithms:
- DBSCAN
- Isolation Forest
Use Cases:
- Fraud detection
- Intrusion detection systems (IDS)
- Insider threat detection
4. Image Compression using PCA
Input:
- High-dimensional image pixel data
Output:
- Lower-dimensional compressed representation
Algorithm:
- Principal Component Analysis (PCA)
Use Cases:
- Reduced storage requirements
- Faster image processing
- Noise reduction
5. Market Basket Analysis
Input:
- Retail transaction data
Output:
- Association rules
- Example: Customers who buy bread also buy milk
Algorithms:
- Apriori
- FP-Growth
Use Cases:
- Product placement optimization
- Cross-selling strategies
- Recommendation systems
Best Practices in Unsupervised Learning
- Data Preprocessing:
Scale features, normalize data, handle missing values - Algorithm Selection:
Choose algorithms based on data type, size, and business goal - Parameter Tuning:
Optimize parameters such as:- Number of clusters (K-Means)
- Epsilon (DBSCAN)
- Evaluation:
Use internal validation metrics (silhouette score, DB index) - Visualization:
Always visualize clusters to validate results - Domain Knowledge:
Interpret clusters using business or domain context - Iterative Process:
Multiple runs and refinements are usually required
Advantages of Unsupervised Learning
- ✔ No labeled data required
- ✔ Discovers hidden patterns
- ✔ Ideal for exploratory data analysis
- ✔ Scales well for large datasets
- ✔ Works across multiple domains
Disadvantages of Unsupervised Learning
- ❌ No ground truth for evaluation
- ❌ Interpretation requires domain expertise
- ❌ Sensitive to parameter selection
- ❌ Can be computationally expensive
- ❌ Results may vary between runs
Evaluation Metrics in Unsupervised Learning
Clustering Quality Metrics
- Silhouette Score
Measures how well a data point fits within its cluster - Davies-Bouldin Index
Measures similarity between clusters (lower is better) - Calinski-Harabasz Index
Ratio of between-cluster dispersion to within-cluster dispersion - Adjusted Rand Index (ARI)
Measures similarity between two clusterings
Dimensionality Reduction Metrics
- Explained Variance Ratio
Percentage of variance preserved by each component - Reconstruction Error
Measures information loss after dimensionality reduction
One-Line Exam Summary 📌
Unsupervised learning discovers hidden patterns in unlabeled data using clustering, dimensionality reduction, and association rule mining to gain insights rather than make predictions.