1. Introduction to Hypothesis Testing
What is Hypothesis Testing?
Hypothesis testing is like playing detective with your data. You make an educated guess (called a hypothesis) about something—like whether one ML model is better than another—and then use math to see if the data supports your guess. It helps you avoid jumping to conclusions based on random patterns.
- Example: You train two models to predict whether a customer will buy a product. Model A gets 85% accuracy, and Model B gets 87%. Is Model B really better, or is the difference just chance? Hypothesis testing gives you the answer.
or
🧠 What is Hypothesis Testing?
Hypothesis testing is a way to make decisions using data. It helps you answer questions like:
- “Is Model A better than Model B?”
- “Does this feature (column) really help predict the output?”
- “Are the results I see due to luck, or are they real?”
It’s like a yes/no test using statistics.
Key Components
Null Hypothesis (H₀):
The “no news” assumption—nothing special is happening.
Example: “Model A and Model B have the same accuracy.”
Formula: Often written as equality,
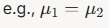
(means are equal)
Alternative Hypothesis (H₁):
- The “something’s up” idea—what you hope to prove.
- Example: “Model B is more accurate than Model A.”
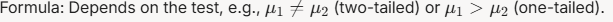
p-value:
- A number telling you how likely your data is if H₀ is true.
- Small p-value (e.g., < 0.05) means H₀ is probably wrong.
- Formula: Not a single equation, but for a test statistic T , it’s
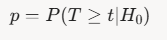
- where t t t is the observed statistic, and the probability comes from a distribution (e.g., t-distribution).
Significance Level (α):
- The cutoff for deciding if the p-value is small enough.
- Usually α=0.05 \alpha = 0.05 α=0.05 (5% risk of being wrong).
- Rule: If p≤α p \leq \alpha p≤α, reject H₀ (your result is significant).
Test Statistic:
- A number summarizing your data to compare against H₀.
- Example: For a t-test, it measures how far apart two means are.
- Formula depends on the test (shown below).
Applications in ML
- Comparing Models: Is a new model better than the old one?
- Feature Significance: Does a feature (like “age”) help predictions?
- Validating Assumptions: Does your data fit a model’s requirements (e.g., normal distribution for linear regression)?
- A/B Testing: Does a new website design get more clicks?
Example
Imagine you’re testing two spam email classifiers:
- Model A: 90% accurate.
- Model B: 92% accurate.
- Question: Is Model B truly better?
- Hypothesis testing checks if the 2% difference is real or just random noise.
2. Types of Hypothesis Tests in ML
There are different tests for different situations. Let’s break them down with formulas and examples.
Parametric Tests
These assume your data follows a pattern, like a normal distribution (bell-shaped curve).
- t-test:
- Compares the means of two groups.
- Types:
- Independent t-test: Two different groups (e.g., Model A on Dataset 1 vs. Model B on Dataset 2).
- Formula:
- Independent t-test: Two different groups (e.g., Model A on Dataset 1 vs. Model B on Dataset 2).


ANOVA (Analysis of Variance):
- Compares means of three or more groups (e.g., Model A, B, C accuracies).
- Formula: F=MSGMSEF = \frac{\text{MSG}}{\text{MSE}}


Z-test:
- Like a t-test but for large samples (e.g., n>30 n > 30 n>30).

p-value: From the standard normal distribution.
Non-Parametric Tests
Use these when data isn’t normal or you’re unsure.
- Mann-Whitney U Test:
- Compares two independent groups (like independent t-test).




Chi-Square Test

Tips
- Parametric: Use if data is normal (check with histograms) and sample size is decent (n>30 n > 30 n>30).
- Non-Parametric: Use for skewed data or small samples.
- Resampling: Great for complex ML models where assumptions are unclear.
- Chi-Square: Perfect for categories (e.g., spam/not spam).
3. Hypothesis Testing in ML Workflow
Hypothesis testing helps at every step of ML:



Example
You’re building a model to predict house prices. You want to know:
- Does the feature “number of bedrooms” matter? (Use t-test or Chi-Square.)
- Is your new model better than the old one? (Use paired t-test.)
- Are your regression residuals normal? (Use Shapiro-Wilk.)



Example
You test if a new feature improves accuracy:




Tips
- Visualize data (e.g., histograms) to check normality.
- Start with simple tests (t-test, Chi-Square).
- Use larger samples for clearer results.

7. Example Use Cases in ML (With Code and Formulas)
Let’s explore five examples (adding one new example for completeness) with formulas, explanations, and Python code. We’ll use synthetic data to keep it simple.

Code:
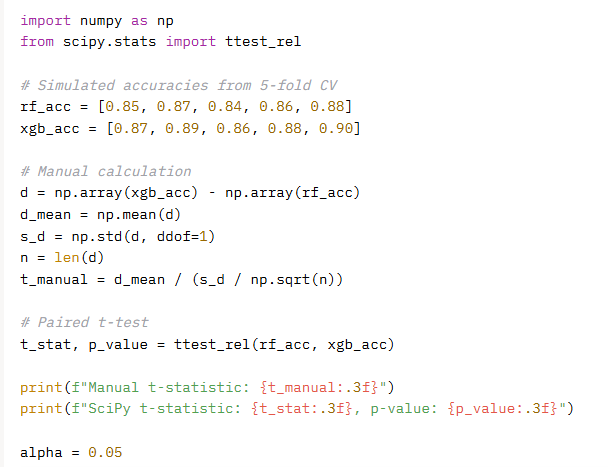


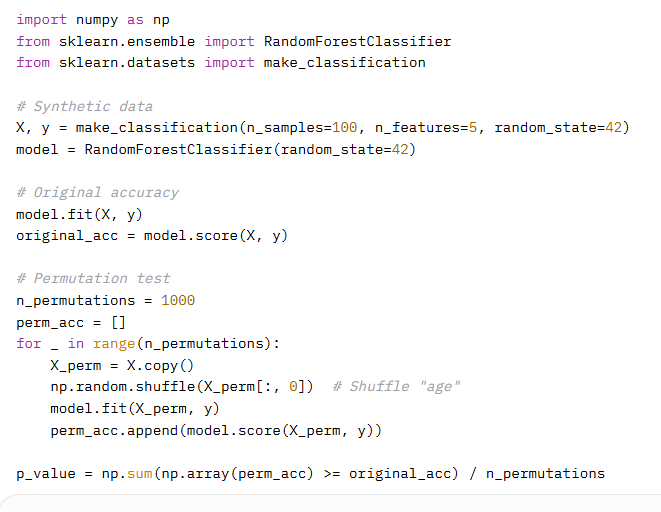
Example 2: Feature Importance (Permutation Test)
Scenario:

Code:
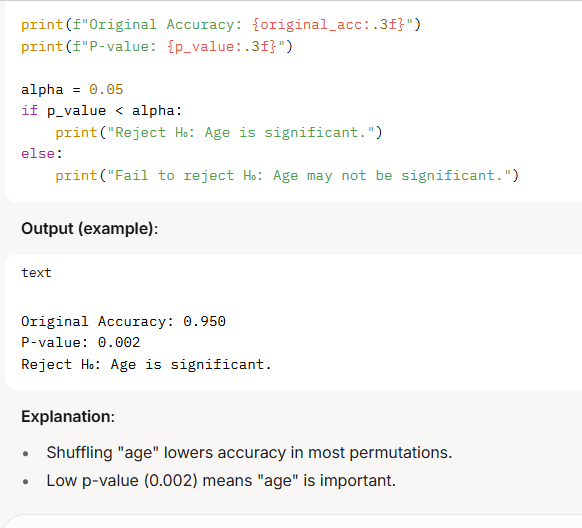
Example 3: A/B Testing (Z-test)
Scenario:

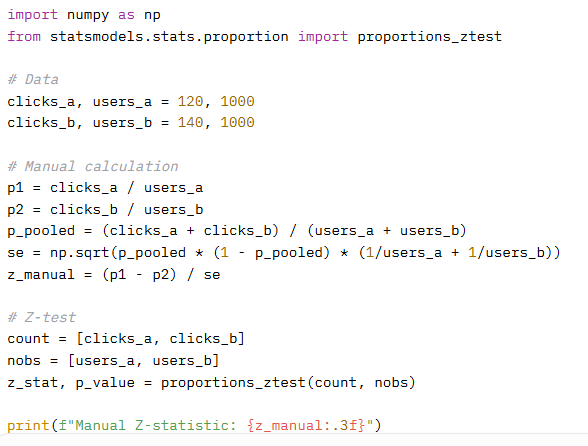
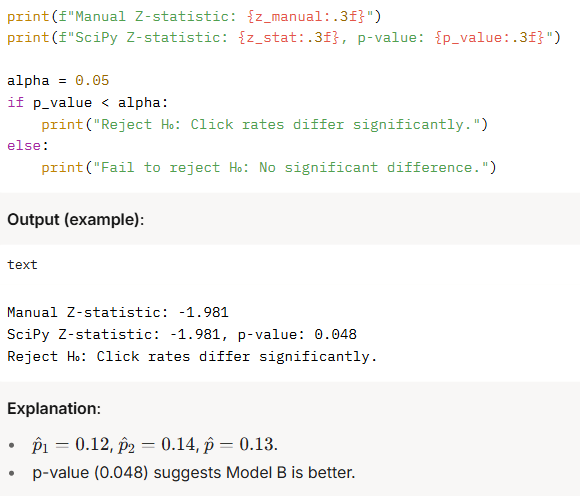
Example 4: Assumption Checking (Shapiro-Wilk Test)
Scenario:

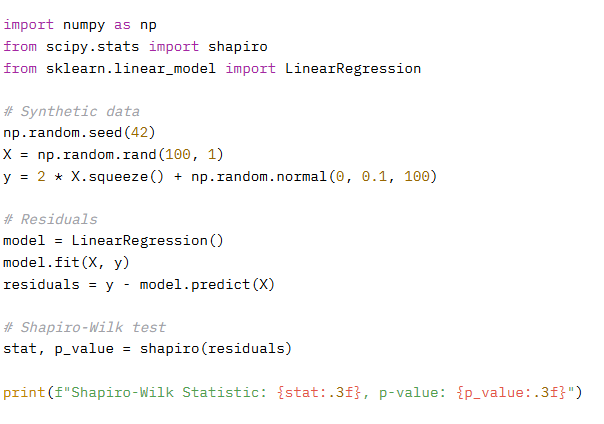
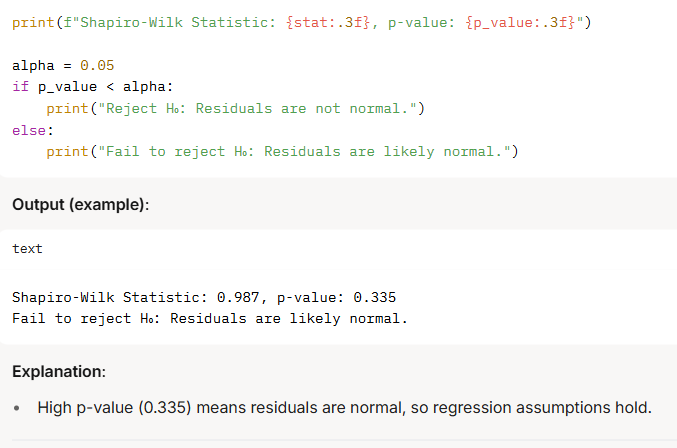
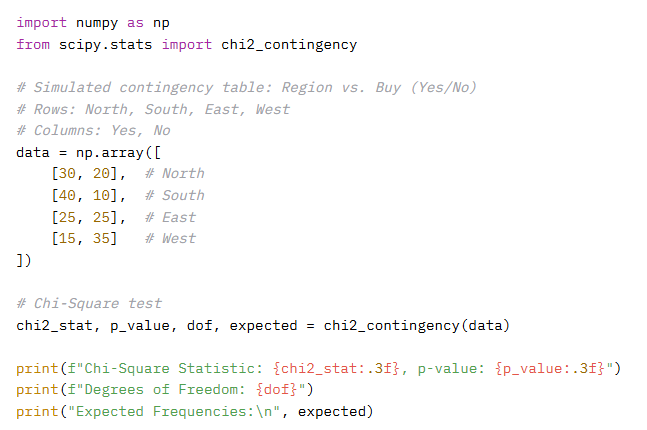
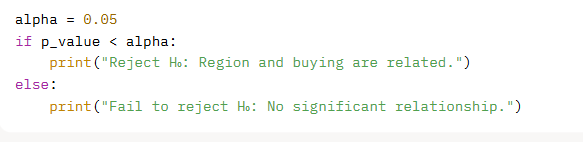
Example 5: Feature Selection (Chi-Square Test) [New Example]
Scenario: