1⭐ Difference Between Supervised and Unsupervised Learning

Machine Learning interviews often start with the question:
“What is the difference between supervised and unsupervised learning?”

Here is a complete, SEO-optimized explanation with definitions, examples, Python code, and sample outputs.

✅ 1. Supervised Learning

Definition

Supervised learning uses labeled data where both input (X) and output (Y) are known.
The model learns a mapping:

f(X) → Y

Goal:

Predict outcomes for new data.

🔥 Types of Supervised Learning

A. Classification

Output: Category
Example: Spam vs Not Spam

B. Regression

Output: Number
Example: House price prediction

🧪 Supervised Learning Example (Classification)

Python Code:

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score

# Load labeled dataset
data = load_iris()
X = data.data
y = data.target

# Train-test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Random Forest model
clf = RandomForestClassifier(n_estimators=100)
clf.fit(X_train, y_train)

# Predict
y_pred = clf.predict(X_test)

# Accuracy
print("Accuracy:", accuracy_score(y_test, y_pred))

📤 Example Output (Typical Output):

Accuracy: 0.9777777777777777

Meaning:
The model correctly predicted 97.7% of flower species.

✅ 2. Unsupervised Learning

Definition

Unsupervised learning works on unlabeled data.
The model identifies:

Patterns
Clusters
Structure

There is no correct answer given during training.

🔥 Types of Unsupervised Learning

A. Clustering

(Group similar items)

B. Dimensionality Reduction

(Simplify data while keeping information)

C. Association

(Find relationships between variables)

🧪 Unsupervised Learning Example (K-Means Clustering)

Python Code:

from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

# Generate synthetic data (unlabeled)
X, _ = make_blobs(n_samples=300, centers=4, random_state=42)

# K-Means clustering
kmeans = KMeans(n_clusters=4)
kmeans.fit(X)

labels = kmeans.predict(X)

print("Cluster Assignments for first 10 rows:", labels[:10])
print("Cluster Centers:\n", kmeans.cluster_centers_)

📤 Example Output (Typical Output):

Cluster Assignments for first 10 rows: [2 3 1 0 1 0 3 2 1 3]

Cluster Centers:
 [[ 1.987  8.964]
 [ -6.879 -6.802]
 [ -2.478  5.003]
 [ 4.696  -6.815]]

Meaning:

Data was automatically divided into 4 clusters
Each cluster has a numerical center

📊 Summary Table: Supervised vs Unsupervised Learning

Feature	Supervised Learning	Unsupervised Learning
Data Type	Labeled	Unlabeled
Goal	Predict outcomes	Discover patterns
Feedback	Yes	No
Tasks	Classification, Regression	Clustering, PCA
Examples	Spam detection	Customer segmentation
Output	Accuracy, error metrics	Clusters, groups
Typical Algorithms	SVM, Random Forest	K-Means, PCA

🎯 When to Use Which?

Use Supervised Learning when:

You have labeled data
You want accurate predictions

Use Unsupervised Learning when:

No labels available
You want to explore data
Labels are expensive

2⭐ Define Overfitting and Underfitting — With Examples

One of the most important concepts in Machine Learning interviews is understanding the difference between overfitting and underfitting.
A good ML model should generalize well — meaning it should perform well not only on the training data but also on unseen data.

🔥 Overfitting vs Underfitting (Simple Definition)

Concept	Meaning
Overfitting	Model learns the training data too well, including noise — performs great on training data but poorly on test data.
Underfitting	Model is too simple and fails to capture patterns — performs poorly on both training and test data.

🎨 Visual Analogy

Imagine fitting a curve through data points:

Scenario	Description
Underfitting	Too simple — e.g., a straight line that misses important trends.
Good Fit	Balanced — captures the true pattern without noise.
Overfitting	Too complex — wiggles through every point, including noise.

✅ 1. Overfitting

Definition

Overfitting happens when a model memorizes the training data — including noise, outliers, and random fluctuations — making it perform poorly on new data.

This results in high variance.

Causes of Overfitting

Model too complex
Too many features
Too many training epochs
Noisy dataset
Small dataset

Symptoms

Very high training accuracy
Low validation/test accuracy

🧪 Example Code: Overfitting (Polynomial Regression)

import numpy as np 
import matplotlib.pyplot as plt 
from sklearn.linear_model import LinearRegression 
from sklearn.preprocessing import PolynomialFeatures 
from sklearn.pipeline import make_pipeline 

# Generate synthetic data 
np.random.seed(0) 
X = np.sort(5 * np.random.rand(20)) 
y = np.sin(X) + np.random.randn(20) * 0.1 

X = X.reshape(-1, 1)

# Overfitting with degree 10 polynomial 
model = make_pipeline(PolynomialFeatures(degree=10), LinearRegression()) 
model.fit(X, y)

# Plot
X_plot = np.linspace(0, 5, 100).reshape(-1, 1)
plt.scatter(X, y, label="Data") 
plt.plot(X_plot, model.predict(X_plot), color='red', label="Overfit Model (Degree 10)") 
plt.title("Overfitting Example") 
plt.legend() 
plt.show()

📤 Expected Output Description

The plotted red curve will wiggle sharply.
The model will nearly pass through every training point.
Curve shows too much flexibility, memorizing noise.

Example training outputs (typical):

Training Score (R²): 0.9999
Test Score (R²): -2.13  # very poor test performance

🛠 How to Reduce Overfitting

✅ 1. Use Simpler Models

Example: reduce polynomial degree, limit tree depth.

✅ 2. Increase Training Data

More data → better generalization.

✅ 3. Regularization (L1/L2)

from sklearn.linear_model import Ridge
ridge = Ridge(alpha=1.0)
ridge.fit(X_train, y_train)

✅ 4. Cross-Validation

from sklearn.model_selection import cross_val_score
scores = cross_val_score(model, X, y, cv=5)

✅ 5. Prune Decision Trees

Limit max_depth, min_samples_split, etc.

✅ 6. Early Stopping (Neural Networks)

✅ 7. Feature Selection

Drop irrelevant features.

📉 2. Underfitting

Definition

Underfitting happens when a model is too simple to understand the underlying patterns in the dataset.

This results in high bias.

Causes of Underfitting

Oversimplified model
Not enough features
Too much regularization
Too little training

Symptoms

Poor performance on both training and test data

🧪 Example Code: Underfitting (Linear Regression)

# Simple linear regression on non-linear data
model = LinearRegression()
model.fit(X, y)

plt.scatter(X, y, label="Data")
plt.plot(X_plot, model.predict(X_plot), color='green', label="Underfit Model (Linear)")
plt.title("Underfitting Example")
plt.legend()
plt.show()

📤 Expected Output Description

The green line will be straight.
It will fail to follow the sine-wave pattern.

Typical output metrics:

Training Score (R²): 0.62
Test Score (R²): 0.55

Both scores are low → model is too simple.

🛠 How to Reduce Underfitting

✅ 1. Increase Model Complexity

Example: use polynomial degree 3 instead of 1.

model = make_pipeline(PolynomialFeatures(degree=3), LinearRegression())
model.fit(X, y)

✅ 2. Add More Features

Feature engineering or additional data attributes.

✅ 3. Reduce Regularization

ridge = Ridge(alpha=0.1)
ridge.fit(X_train, y_train)

✅ 4. Train Longer / Improve Optimization

Increase epochs for neural networks.

✅ 5. Use More Powerful Algorithms

Random Forest, Gradient Boosting, Neural Networks.

📊 Summary Table — Overfitting vs Underfitting

Aspect	Overfitting	Underfitting
Train Performance	High	Low
Test Performance	Low	Low
Error Type	High variance	High bias
Cause	Too complex	Too simple
Solution	Simplify model	Make model more complex
Learns Noise?	Yes	No
Generalization	Poor	Poor

🧠 Practical Tips to Avoid Both

Start simple, increase complexity gradually
Track training & validation performance
Use learning curves
Apply proper regularization
Engineer meaningful features

✅ Conclusion

Overfitting → model is too complex and memorizes noise
Underfitting → model is too simple and misses patterns
Achieving the right balance leads to high-performance ML models.

3. Explain the Bias-Variance Tradeoff

The bias-variance tradeoff is a fundamental concept in machine learning that explains the balance between model simplicity and model flexibility.

🔹 Bias

Error due to overly simplistic assumptions.
A high-bias model cannot capture patterns well → Underfitting.

🔹 Variance

Error due to too much sensitivity to training data.
A high-variance model learns noise → Overfitting.

📊 Bias-Variance Comparison Table

Model Type	Bias	Variance	Performance
High Bias	High	Low	Underfits
High Variance	Low	High	Overfits
Optimal Model	Low	Low	Best generalization

🎯 Goal of the Tradeoff

Find a balanced model that:
✔ captures important patterns (low bias)
✔ generalizes well to new data (low variance)

📌 Examples

Linear Regression on a highly nonlinear dataset → High bias (underfitting)
Deep Neural Network with a small dataset → High variance (overfitting)

4. What Is the Curse of Dimensionality?

The curse of dimensionality refers to challenges that arise when the number of input features (dimensions) increases.

📉 Why It Is a Problem

As dimensions increase:

The feature space expands exponentially
Data becomes sparse, making learning difficult
Distance metrics stop working well (all points appear similar)
Models struggle to generalize → poor performance
Computation and training time increase drastically

🔧 Solutions to the Curse of Dimensionality

✔ 1. Dimensionality Reduction

PCA (Principal Component Analysis)
t-SNE (for visualization)
Autoencoders

✔ 2. Feature Selection

Remove irrelevant or redundant features
Methods:
- Filter methods (chi-square, ANOVA)
- Wrapper methods (RFE)
- Embedded methods (Lasso)

✔ 3. Regularization

L1 (Lasso) → forces feature elimination
L2 (Ridge) → reduces feature influence

5. How Do You Handle Missing or Corrupted Data in a Dataset?

Handling missing data is a crucial preprocessing step in any machine learning pipeline. Poor handling can lead to biased models, reduced accuracy, and incorrect insights. Below are the most commonly used strategies.

✅ 1. Remove Missing Data (Rows or Columns)

Useful when the percentage of missing values is small.

Remove Rows With Missing Values

df.dropna()  # Removes rows containing any missing value

Remove Columns With Many Missing Values

df.drop(columns=['col_with_missing'])

✔ Best suited when missing data is minimal
✔ Avoids introducing artificial values
✖ Not recommended when a lot of data is missing

✅ 2. Impute Missing Values

Imputation fills in missing values based on statistics or ML models.

A. Simple Imputation Methods

Mean / Median → Numerical features
Mode → Categorical features

Example: Mean Imputation Using Scikit-Learn

from sklearn.impute import SimpleImputer

imputer = SimpleImputer(strategy='mean')
df['column'] = imputer.fit_transform(df[['column']])

B. Advanced Imputation

KNN Imputer
Iterative Imputer
Predict missing values using a machine learning model

✔ Preserves dataset size
✔ Works well when missingness is not random

✅ 3. Use Algorithms That Handle Missing Data Automatically

Some models can natively handle missing values, such as:

XGBoost
LightGBM
CatBoost

These algorithms learn the best direction to route missing values during tree splits.

✔ No manual imputation required
✔ Higher accuracy for complex datasets

✅ 4. Create a “Missing Indicator” Feature

This technique adds a binary column to indicate whether a value was missing.

Example:

df['column_missing_flag'] = df['column'].isna().astype(int)

Why it helps:

Missingness itself may carry important information (e.g., customer not providing salary).

6. What Is the Difference Between Classification and Regression?

Classification and regression are two fundamental types of supervised machine learning problems. The key difference lies in the output they predict.

📌 Classification vs Regression (Quick Comparison)

Feature	Classification	Regression
Output	Discrete class label	Continuous numeric value
Objective	Predict which category an observation belongs to	Predict a real-valued quantity
Evaluation Metrics	Accuracy, Precision, Recall, F1-score, ROC-AUC	MAE, MSE, RMSE, R²
Examples	Spam detection, Disease prediction, Image recognition	House prices, Stock prices, Temperature prediction

🔍 Simple Summary:

Classification → What category does it belong to?
Regression → What is the value?

7. Describe the Steps Involved in Building a Machine Learning Model

Building an ML model involves a systematic pipeline to ensure accuracy, reliability, and generalization.

🔟 Machine Learning Workflow (Step-by-Step)

1. Problem Definition

Understand the business objective
Identify whether it’s classification, regression, clustering, etc.

2. Data Collection

Collect data from databases, CSVs, APIs, sensors, web scraping, etc.

3. Data Preprocessing

Handle missing values
Remove duplicates and outliers
Encode categorical variables
Normalize/standardize features

4. Exploratory Data Analysis (EDA)

Understand feature distributions
Plot correlations and trends
Detect patterns and anomalies

5. Feature Engineering

Create new meaningful features
Select relevant features
Transform existing data (log, polynomial, scaling)

6. Train/Test Split

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

7. Model Selection & Training

Choose an algorithm (Linear Regression, SVM, Decision Tree, etc.)
Fit the model to training data

8. Model Evaluation

Use appropriate metrics based on the problem type
Compare performance on test data

9. Hyperparameter Tuning

Use Grid Search, Random Search, or Bayesian Optimization

10. Deployment & Monitoring

Deploy using APIs, cloud, or applications
Monitor for data drift, decay, and update when needed

8. What Are the Assumptions of Linear Regression?

Linear regression works well only when its core assumptions hold true.

📌 Linear Regression Assumptions

1. Linearity

The relationship between independent variables (X) and the target variable (Y) is linear.

2. Independence

Observations should be independent of each other.

3. Homoscedasticity

Residuals (errors) must have constant variance.
(No increasing or decreasing spread in errors)

4. Normality of Errors

Residuals should follow a normal distribution.

5. No Multicollinearity

Features should not be highly correlated with each other.
(High multicollinearity distorts coefficients)

⚠️ If these assumptions are violated:

Coefficients may be unreliable
Model accuracy can drop
Interpretability becomes flawed

9. How Do You Evaluate the Performance of a Regression Model?

Evaluating a regression model helps measure how accurately it predicts continuous numerical values. Below are the most common and widely used regression evaluation metrics.

✅ 1. Mean Absolute Error (MAE)

Measures the average absolute difference between predicted and actual values.

Easy to understand
Less sensitive to outliers than MSE

✅ 2. Mean Squared Error (MSE)

Measures the average squared error between actual and predicted values.

Penalizes larger errors heavily
Good for optimization

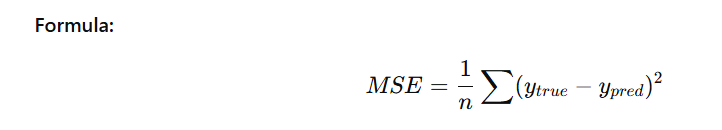
✅ 3. Root Mean Squared Error (RMSE)

Square root of MSE.
Gives error in the same units as the target variable.

More sensitive to outliers than MAE
Easy to interpret

✅ 4. R-Squared (R² Score)

Measures how well the model explains the variance in the target.

1 → Perfect fit
0 → Model predicts no better than mean
Negative → Very poor model

📌 Python Example: Regression Model Evaluation

from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score

# Example values: Replace y_true, y_pred with your own arrays
# y_true = [...]
# y_pred = [...]

mae = mean_absolute_error(y_true, y_pred)
mse = mean_squared_error(y_true, y_pred)
rmse = mean_squared_error(y_true, y_pred, squared=False)
r2 = r2_score(y_true, y_pred)

print(f"MAE: {mae}")
print(f"MSE: {mse}")
print(f"RMSE: {rmse}")
print(f"R² Score: {r2}")

🔍 Quick Summary Table

Metric	Measures	Best Value	Notes
MAE	Avg. absolute error	0	Less sensitive to outliers
MSE	Avg. squared error	0	Penalizes large errors
RMSE	Standard deviation of prediction errors	0	Same units as target
R²	Variance explained	1	Can be negative

10. What Is Cross-Validation, and Why Is It Important?

Cross-validation is a model validation technique used to evaluate how well a machine learning model generalizes to unseen data. Instead of relying on a single train-test split, cross-validation uses multiple folds to provide a more reliable performance estimate.

⭐ K-Fold Cross-Validation (Most Popular Method)

How it works:

Split the dataset into k equal subsets (folds).
Train the model on k−1 folds.
Test on the remaining fold.
Repeat the process k times with a different fold each time.
Average the scores → final performance metric.

This reduces bias and variance caused by a single split.

✅ Python Example:

from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression

model = LinearRegression()
scores = cross_val_score(model, X, y, cv=5, scoring='neg_mean_squared_error')
mse_scores = -scores
print("Average MSE:", mse_scores.mean())

⭐ Why Cross-Validation Is Important

✔ More reliable than a single train-test split
✔ Helps detect overfitting and underfitting
✔ Ensures the model performs well on different subsets
✔ Reduces variance in performance estimates

Cross-validation is essential for model selection, comparing algorithms, and hyperparameter tuning.

11. How Does the k-Nearest Neighbors (k-NN) Algorithm Work?

k-Nearest Neighbors (k-NN) is a simple, non-parametric, instance-based algorithm used for classification and regression.

⭐ How k-NN Works

Store the entire training dataset.
For a new input, calculate the distance (e.g., Euclidean) to all training points.
Select the k closest neighbors.
Predict:
- Classification: majority vote
- Regression: average of the k neighbors

⭐ Pros and Cons of k-NN

Pros	Cons
Simple and intuitive	Slow for large datasets
No training time	Sensitive to scale and irrelevant features
Works well for small datasets	High memory usage

⭐ Python Example:

from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

# Load dataset
iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(
    iris.data, iris.target, test_size=0.3)

# Train model
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train)

# Predict & accuracy
print("Accuracy:", knn.score(X_test, y_test))

12. What Is the Difference Between Decision Trees and Random Forests?

Decision Trees and Random Forests are both popular machine learning algorithms, but they differ significantly in performance and structure.

⭐ Decision Tree vs. Random Forest: Key Differences

Feature	Decision Tree	Random Forest
Model Type	Single tree	Ensemble of many trees
Training	Trained on full dataset	Each tree trained on random bootstrap samples
Overfitting	High risk	Reduced via averaging
Variance	High	Low
Accuracy	Moderate	Higher
Interpretability	Very interpretable	Less interpretable

⭐ Why Random Forest Performs Better

Random Forest reduces overfitting by:

Training multiple decision trees
Using bootstrapped samples
Randomly selecting features for splitting

This creates more stable and generalizable predictions.

⭐ Python Example:

from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier

# Decision Tree
dt = DecisionTreeClassifier()
dt.fit(X_train, y_train)

# Random Forest
rf = RandomForestClassifier(n_estimators=100)
rf.fit(X_train, y_train)

print("DT Accuracy:", dt.score(X_test, y_test))
print("RF Accuracy:", rf.score(X_test, y_test))

13. Explain How the Support Vector Machine (SVM) Algorithm Works

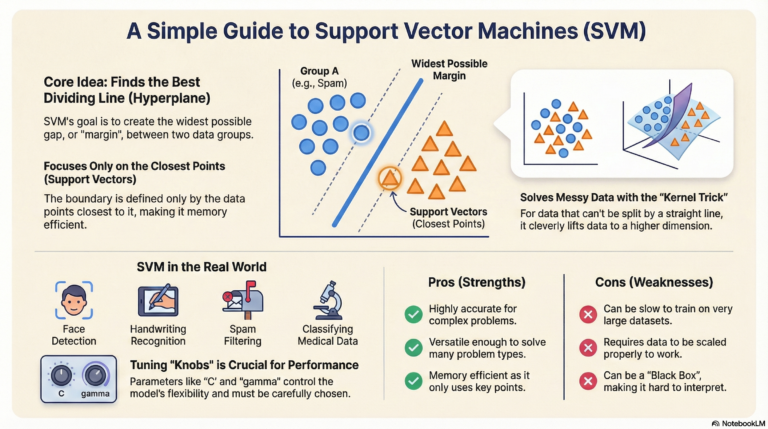
Support Vector Machine (SVM) is a powerful supervised learning algorithm used for classification and regression. Its main goal is to find the optimal hyperplane that best separates different classes.

⭐ How SVM Works

1. Find the Optimal Hyperplane

SVM chooses a hyperplane that maximizes the margin — the distance between the separating hyperplane and the nearest data points.

2. Support Vectors

The closest data points to the hyperplane are called support vectors.
These points determine the decision boundary.

3. Soft Margin vs Hard Margin

Type	Description
Hard Margin	Forces perfect classification; can overfit; works only if data is linearly separable
Soft Margin	Allows misclassification for better generalization; used in real-world data

4. Kernel Trick

If data is not linearly separable, SVM uses kernels to map data into a higher-dimensional space.

⭐ Code Example: Linear SVM

from sklearn.svm import SVC

svm = SVC(kernel='linear')
svm.fit(X_train, y_train)

print("Accuracy:", svm.score(X_test, y_test))

14. What Is the Purpose of the Kernel Trick in SVM?

The kernel trick allows SVM to handle non-linear classification problems by implicitly mapping inputs into higher-dimensional space without computing the actual transformation.

This makes SVM powerful even with complex datasets.

⭐ Example: RBF Kernel

svm_rbf = SVC(kernel='rbf')
svm_rbf.fit(X_train, y_train)

print("RBF Kernel Accuracy:", svm_rbf.score(X_test, y_test))

15. Describe the Naive Bayes Classifier and Its Assumptions

Naive Bayes is a probabilistic classifier based on Bayes’ Theorem.
It is called “naive” because it assumes that all features are independent given the class label.

⭐ Assumptions of Naive Bayes

Features are conditionally independent
All features contribute equally
Works best with high-dimensional data (NLP, spam detection)

⭐ Types of Naive Bayes

Type	Use Case
GaussianNB	Continuous features (normal distribution)
MultinomialNB	Text classification, word counts
BernoulliNB	Binary features (0/1)

⭐ Code Example

from sklearn.naive_bayes import GaussianNB

gnb = GaussianNB()
gnb.fit(X_train, y_train)

print("Accuracy:", gnb.score(X_test, y_test))

16. How Does the K-Means Clustering Algorithm Work?

K-Means is an unsupervised clustering algorithm that divides data into k clusters.

⭐ Steps of K-Means

Initialize k centroids randomly
Assign each point to its nearest centroid
Recalculate centroids as the mean of all assigned points
Repeat until:
- Centroids stop moving
- Max iterations reached

⭐ Code Example

from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

X, y_true = make_blobs(n_samples=300, centers=4, random_state=42)

kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
labels = kmeans.predict(X)

17. What Are the Limitations of K-Means Clustering?

Although K-Means is popular, it has several important limitations.

⭐ Limitations of K-Means

Limitation	Explanation
Must specify k	Requires defining number of clusters beforehand
Sensitive to initialization	Poor starting centroids → poor clusters
Sensitive to outliers	Outliers distort cluster centers heavily
Assumes spherical clusters	Fails on irregular or elongated clusters
Not good for high-dimensional data	Suffers from curse of dimensionality
Bad for uneven cluster sizes	Prefers equal-sized clusters

18️⃣ What is Hierarchical Clustering?

Hierarchical Clustering builds a tree-like hierarchy of clusters using a dendrogram 🌳.

Types:

🔹 Agglomerative (Bottom-Up) → Start with each point → merge clusters
🔹 Divisive (Top-Down) → Start with one large cluster → split

Linkage Methods:

✔ Single Linkage → min distance
✔ Complete Linkage → max distance
✔ Average Linkage → average distance
✔ Ward Linkage → minimizes intra-cluster variance

Python Example:

from scipy.cluster.hierarchy import dendrogram, linkage
import matplotlib.pyplot as plt

Z = linkage(X, method='ward')
plt.figure(figsize=(10, 5))
dendrogram(Z)
plt.title("Dendrogram")
plt.show()

19️⃣ What is Principal Component Analysis (PCA)?

PCA is a dimensionality reduction technique that transforms features into principal components that capture maximum variance 📉➡📈.

What PCA Does:

✔ Removes noise
✔ Handles multicollinearity
✔ Reduces dimensions while keeping max info
✔ Helps visualize high-dim datasets (2D/3D)

Steps:

1️⃣ Standardize data
2️⃣ Compute covariance matrix
3️⃣ Get eigenvalues & eigenvectors
4️⃣ Select top components
5️⃣ Transform data

Code Example:

from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler

X_scaled = StandardScaler().fit_transform(X)
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)

20️⃣ How Does PCA Reduce Dimensionality?

PCA keeps only the components with highest variance, dropping low-information features → making models faster, simpler, and often more accurate 🤖⚡

Benefits:

🔹 Reduces computation time
🔹 Removes correlated features
🔹 Helps visualization
🔹 Acts as noise filter

Check Explained Variance:

print(pca.explained_variance_ratio_)

✅ Quick Summary Table

Algorithm	Type	Use Case	Pros	Cons
k-NN	Supervised	Classification/Regression	Simple	Slow for large data
Decision Tree	Supervised	Any	Interpretable	Overfitting
Random Forest	Supervised	Any	Robust	Less interpretable
SVM	Supervised	Classification	Great for high-dim	Sensitive to kernels
Naive Bayes	Supervised	Text	Fast	Independence assumption
K-Means	Unsupervised	Clustering	Fast	Sensitive to k
Hierarchical Clustering	Unsupervised	Clustering	Visual	Heavy for large data
PCA	Unsupervised	Dimensionality Reduction	Reduces complexity	Harder to interpret

21️⃣ What is a Confusion Matrix?

A confusion matrix is a table that compares actual vs predicted values to evaluate classification performance.

Binary Classification Layout:

	Predicted: No	Predicted: Yes
Actual: No	TN	FP
Actual: Yes	FN	TP

Meaning:

TP → Correctly predicted positive
TN → Correctly predicted negative
FP → Predicted positive but actually negative
FN → Predicted negative but actually positive

Python Code:

from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
import matplotlib.pyplot as plt

y_true = [1, 0, 1, 1, 0, 1]
y_pred = [1, 0, 0, 1, 0, 1]

cm = confusion_matrix(y_true, y_pred)
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=['No', 'Yes'])
disp.plot()
plt.title("Confusion Matrix")
plt.show()

22️⃣ Precision, Recall, and F1-Score

Derived directly from the confusion matrix.

Python Code:

from sklearn.metrics import precision_score, recall_score, f1_score

precision = precision_score(y_true, y_pred)
recall = recall_score(y_true, y_pred)
f1 = f1_score(y_true, y_pred)

print(f"Precision: {precision}, Recall: {recall}, F1 Score: {f1}")

23️⃣ What is the ROC Curve?

The ROC (Receiver Operating Characteristic) curve plots:

TPR (Recall) vs
FPR at different thresholds.

Interpretation:

Curve close to top-left → excellent model
Diagonal line → random guessing

Python Code:

from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt

fpr, tpr, thresholds = roc_curve(y_true, y_scores)
plt.plot(fpr, tpr, label='ROC Curve')
plt.plot([0, 1], [0, 1], 'k--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend()
plt.show()

24️⃣ What is AUC-ROC?

AUC = Area Under the ROC Curve

Meaning:

1.0 → Perfect classifier
0.5 → Random guess
> 0.5 → Useful model

AUC measures the overall ability to distinguish between classes.

Code:

from sklearn.metrics import roc_auc_score

auc = roc_auc_score(y_true, y_scores)
print(f"AUC-ROC Score: {auc}")

25️⃣ Choosing the Right Evaluation Metric

Depends on your domain + cost of mistakes.

📌 Recommended Metrics Based on Problem:

Scenario	Best Metric
Balanced data	Accuracy
Imbalanced data	Precision, Recall, F1, AUC
Medical diagnosis (avoid FN)	Recall
Spam detection (avoid FP)	Precision
Multi-class	Macro/Micro F1, Accuracy
Need probability quality	Log Loss, AUC

Example:

🔹 Medical tests: Missing a disease = worst → choose Recall
🔹 Spam filtering: Marking important email as spam = worst → choose Precision

26️⃣ Difference Between L1 & L2 Regularization

Feature	L1 (Lasso)	L2 (Ridge)
Penalty	( \lambda \sum	w_i
Sparsity	Produces sparse models (sets weights → 0)	Shrinks weights, does not zero them
Use Case	Feature selection	Prevent overfitting
Optimization	Not differentiable at 0	Smooth & differentiable
Effect	Removes irrelevant features	Stabilizes weights

Python Code

from sklearn.linear_model import Lasso, Ridge

# L1 Regularization (Lasso)
lasso = Lasso(alpha=0.1)
lasso.fit(X_train, y_train)

# L2 Regularization (Ridge)
ridge = Ridge(alpha=0.1)
ridge.fit(X_train, y_train)

27️⃣ How to Handle Imbalanced Datasets

When one class dominates heavily (e.g., fraud detection).

Techniques:

✅ 1. Resampling

Oversampling → SMOTE
Undersampling → remove majority samples

from imblearn.over_sampling import SMOTE
smote = SMOTE()
X_res, y_res = smote.fit_resample(X, y)

✅ 2. Use Correct Metrics

F1-score
Precision/Recall
AUC-ROC

✅ 3. Class Weighting

from sklearn.linear_model import LogisticRegression
model = LogisticRegression(class_weight='balanced')

✅ 4. Ensemble Models

Random Forest
XGBoost (scale_pos_weight)

✅ 5. Anomaly Detection

For extremely rare positive classes.

28️⃣ Purpose of a Learning Curve

A learning curve shows model performance as training data increases.

📌 Helps identify:

Underfitting (both curves low)
Overfitting (large gap between curves)
Whether adding more data helps

Python Code

from sklearn.model_selection import learning_curve
import numpy as np
import matplotlib.pyplot as plt

train_sizes, train_scores, test_scores = learning_curve(
    estimator=model,
    X=X, y=y,
    train_sizes=np.linspace(0.1, 1.0, 10),
    cv=5,
    scoring="accuracy"
)

train_mean = train_scores.mean(axis=1)
test_mean = test_scores.mean(axis=1)

plt.plot(train_sizes, train_mean, label='Training score')
plt.plot(train_sizes, test_mean, label='Validation score')
plt.xlabel('Training Set Size')
plt.ylabel('Accuracy')
plt.title('Learning Curve')
plt.legend()
plt.show()

29️⃣ Detecting & Fixing Multicollinearity

Multicollinearity = independent variables are highly correlated, causing unstable coefficients.

How to detect:

🔹 1. Correlation Matrix

Look for > 0.8 correlations.

🔹 2. VIF — Variance Inflation Factor

VIF > 10 = Serious multicollinearity
VIF > 5 = Warning

VIF Code

from statsmodels.stats.outliers_influence import variance_inflation_factor
import pandas as pd

def compute_vif(df):
    vif_data = pd.DataFrame()
    vif_data["Feature"] = df.columns
    vif_data["VIF"] = [variance_inflation_factor(df.values, i)
                       for i in range(df.shape[1])]
    return vif_data

vif_df = compute_vif(X)
print(vif_df)

Fixes:

Remove correlated features
Use PCA
Use regularization (L1/L2)
Combine features

30️⃣ Difference Between Bagging & Boosting

Feature	Bagging	Boosting
Type	Parallel ensemble	Sequential ensemble
Goal	Reduce variance	Reduce bias
Training	Independent models	Each model fixes previous errors
Best For	High-variance models	Weak models needing improvement
Robustness	Good with noisy data	Sensitive to outliers
Examples	Random Forest	AdaBoost, XGBoost, Gradient Boosting

Bagging Example (Random Forest)

from sklearn.ensemble import RandomForestClassifier

rf = RandomForestClassifier(n_estimators=100)
rf.fit(X_train, y_train)

Boosting Example (AdaBoost)

from sklearn.ensemble import AdaBoostClassifier

ada = AdaBoostClassifier(n_estimators=100)
ada.fit(X_train, y_train)

31. What is feature engineering, and why is it important?

Definition:

Feature engineering is the process of creating, transforming, or selecting features from raw data to improve the performance of machine learning models.

Why It’s Important:

✔ Improves model accuracy and generalization
✔ Helps algorithms learn patterns more effectively
✔ Reduces overfitting by removing unnecessary features
✔ Speeds up training time and convergence
✔ Makes the model more interpretable

Common Feature Engineering Techniques:

Creating new features (ratios, interactions, polynomial features)
Transformations (log, square root, scaling)
Binning continuous variables
Encoding categorical features
Handling missing values
Feature selection (filter, wrapper, embedded methods)

32. How do you handle categorical variables in a dataset?

Categorical variables must be converted to numeric form before model training.

Encoding Techniques:

Method	Description	Best For
Label Encoding	Assigns an integer to each category	Ordinal data (Low < Medium < High)
One-Hot Encoding	Creates binary column for each category	Nominal data (no order)
Target Encoding	Replaces category with target mean	High-cardinality features (hundreds of categories)

Code Example:

from sklearn.preprocessing import LabelEncoder

le = LabelEncoder()
df['category_encoded'] = le.fit_transform(df['category'])

33. What is one-hot encoding?

One-hot encoding converts a categorical variable into multiple binary indicator variables.

Example:

Color	red	green	blue
red	1	0	0
green	0	1	0
blue	0	0	1

Code Examples:

Using Pandas

df_encoded = pd.get_dummies(df, columns=['color'])

Using Scikit-learn

from sklearn.preprocessing import OneHotEncoder
encoder = OneHotEncoder()
encoded_features = encoder.fit_transform(df[['color']])

34. Explain the concept of feature scaling and normalization.

Feature scaling transforms numerical values into a standard range so that each feature contributes equally.

Why It Is Needed

Prevents dominance of large-range features
Essential for distance-based algorithms:
✔ k-NN, ✔ SVM, ✔ K-Means
Required for gradient descent (Neural networks)

Common Techniques:

Min-Max Scaling (Normalization) → range [0, 1]
Standardization (Z-score Scaling) → mean 0, variance 1

35. Difference between Normalization and Standardization

Feature	Normalization (Min-Max)	Standardization (Z-score)
Formula	(x − min) / (max − min)	(x − μ) / σ
Range	[0, 1]	No fixed range
Sensitive to outliers	Yes	Less sensitive
When to use	When data is not normal	When data follows Gaussian distribution

Code Example:

from sklearn.preprocessing import MinMaxScaler, StandardScaler

# Normalization
minmax_scaler = MinMaxScaler()
X_norm = minmax_scaler.fit_transform(X)

# Standardization
std_scaler = StandardScaler()
X_std = std_scaler.fit_transform(X)

36. How do you deal with outliers in your data?

Outliers can negatively affect model accuracy, especially in linear models and distance-based algorithms.

Detection Methods

Boxplot & IQR Rule
- Outlier if:
  - x < Q1 – 1.5 × IQR
  - x > Q3 + 1.5 × IQR
Z-score Method
- Values with |Z| > 3 considered outliers
Visualization
- Scatter plots
- Histograms
- Boxplots

Treatment Options

Remove outliers
Cap/Floor extreme values (Winsorization)
Apply transformations (log, sqrt)
Use RobustScaler to reduce outlier impact
Replace outliers with median/percentile values

Code Example

from scipy.stats import zscore
import numpy as np

# Z-score method
df_cleaned = df[(np.abs(zscore(df)) < 3).all(axis=1)]

# IQR method
Q1 = df.quantile(0.25)
Q3 = df.quantile(0.75)
IQR = Q3 - Q1
df_cleaned = df[~((df < (Q1 - 1.5*IQR)) | (df > (Q3 + 1.5*IQR))).any(axis=1)]

37. What is feature selection, and how is it performed?

Definition

Feature selection is the process of selecting the most relevant features to improve model performance and reduce dimensionality.

Why It’s Important

Faster training
Reduces overfitting
Improves accuracy
Increases interpretability

Feature Selection Approaches

Method	Description	Examples
Filter Methods	Select features based on statistical tests	Correlation, Chi-square
Wrapper Methods	Test subsets using a model	RFE, Forward/Backward selection
Embedded Methods	Done inside the model training process	Lasso (L1), Decision Trees

38. Describe the Recursive Feature Elimination (RFE) method.

RFE is a wrapper feature selection technique that removes features recursively based on model importance.

Steps

Train a model
Rank features by importance
Remove the least important feature(s)
Repeat until the desired number of features is reached

Code Example

from sklearn.feature_selection import RFE
from sklearn.ensemble import RandomForestClassifier

model = RandomForestClassifier()
rfe = RFE(estimator=model, n_features_to_select=5)
X_selected = rfe.fit_transform(X, y)

39. How does regularization help in feature selection?

Regularization adds a penalty to large coefficients and helps reduce overfitting.

L1 Regularization (Lasso)

Encourages sparsity
Sets some coefficients exactly zero
Automatically performs feature selection

L2 Regularization (Ridge)

Shrinks coefficients
Does not eliminate them
Helps reduce variance but not used for feature selection

Code Example

from sklearn.linear_model import Lasso

lasso = Lasso(alpha=0.1)
lasso.fit(X_train, y_train)

# Selected features (non-zero coefficients)
selected_features = X.columns[lasso.coef_ != 0]

40. What is the role of domain knowledge in feature engineering?

Domain knowledge helps create meaningful and relevant features.

Importance of Domain Knowledge

Determines useful transformations
Avoids irrelevant or misleading features
Helps design interaction or derived features
Improves model interpretability

Examples

Healthcare: BMI bins, age groups, risk scores
Finance: Volatility, rolling averages, stock returns
NLP: TF-IDF, sentiment analysis, keyword density
Time Series: Lag features, moving averages, day-of-week

41. What is hyperparameter tuning?

Hyperparameters are parameters set before training (example: learning rate, number of trees, max depth) and not learned from data.

Hyperparameter Tuning

The process of finding the best hyperparameter combination to maximize model performance.

Why It’s Important

Greatly improves accuracy
Prevents underfitting & overfitting
Optimizes training time and model complexity

42. Describe the grid search method for hyperparameter tuning.

Grid Search performs an exhaustive search through all possible hyperparameter combinations.

How It Works

Define a grid of parameters
Train the model for every combination
Use cross-validation to evaluate each
Select the best parameters

Code Example

from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import RandomForestClassifier

param_grid = {
    'n_estimators': [50, 100],
    'max_depth': [None, 10, 20],
    'min_samples_split': [2, 5]
}

grid_search = GridSearchCV(
    RandomForestClassifier(),
    param_grid,
    cv=5,
    scoring='accuracy'
)

grid_search.fit(X_train, y_train)

print("Best Parameters:", grid_search.best_params_)
print("Best Score:", grid_search.best_score_)

43. What is random search, and how does it differ from grid search?

Random Search selects random combinations of hyperparameters instead of testing all.

Key Differences

Feature	Grid Search	Random Search
Search Type	Exhaustive	Random sampling
Speed	Slow for large grids	Faster, scalable
Coverage	Tests all combinations	May skip some
Useful When	Small grid	Large search space

Code Example

from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint, uniform
from sklearn.ensemble import RandomForestClassifier

param_dist = {
    'n_estimators': randint(50, 200),
    'max_depth': [None, 10, 20, 30],
    'min_samples_split': uniform(0.1, 0.9)
}

random_search = RandomizedSearchCV(
    RandomForestClassifier(),
    param_dist,
    n_iter=30,
    cv=5,
    scoring='accuracy'
)

random_search.fit(X_train, y_train)

print("Best Parameters:", random_search.best_params_)

44. Explain the concept of early stopping in model training.

Early stopping is a regularization technique that stops training when the validation loss stops improving.

How It Works

Evaluate validation loss each epoch
If no improvement for N epochs (patience), stop
Restore the best weights

Benefits

Prevents overfitting
Reduces training time
Produces a more generalizable model

Code Example (Keras)

from tensorflow.keras.callbacks import EarlyStopping

early_stop = EarlyStopping(
    monitor='val_loss',
    patience=5,
    restore_best_weights=True
)

history = model.fit(
    X_train,
    y_train,
    epochs=100,
    validation_split=0.2,
    callbacks=[early_stop]
)

45. How do you prevent overfitting in a model?

Overfitting happens when the model memorizes training data patterns—including noise—leading to poor generalization.

Techniques to Prevent Overfitting

Method	Description
Regularization (L1/L2)	Limits large weights
Cross-validation	Ensures generalization
Pruning	Simplifies decision trees
Dropout	Randomly removes neurons in neural nets
Data Augmentation	Creates more training samples
Reduce Model Complexity	Use simpler models
Early Stopping	Stop training when no improvement

46. What is dropout in neural networks?

Dropout is a regularization technique used in deep learning to reduce overfitting.

How It Works

During training, randomly drops (deactivates) a fraction of neurons.
Prevents the network from relying too much on specific neurons.
Forces the model to learn redundant, generalized representations.
During inference, all neurons are used but their outputs are scaled to maintain balance.

Code Example (Keras)

from tensorflow.keras.layers import Dense, Dropout
from tensorflow.keras.models import Sequential

model = Sequential([
    Dense(128, activation='relu'),
    Dropout(0.5),  # 50% dropout
    Dense(64, activation='relu'),
    Dropout(0.5),
    Dense(1, activation='sigmoid')
])

47. How does batch normalization work?

Batch Normalization (BatchNorm) normalizes the inputs of each layer to stabilize and speed up training.

Why It Helps

Faster training & better convergence
Reduces dependency on weight initialization
Acts as a regularizer and reduces overfitting

How It Works (per mini-batch)

Code Example (Keras)

from tensorflow.keras.layers import Dense, BatchNormalization, Activation
from tensorflow.keras.models import Sequential

model = Sequential([
    Dense(128),
    BatchNormalization(),
    Activation('relu'),
    Dense(64),
    BatchNormalization(),
    Activation('relu'),
    Dense(1, activation='sigmoid')
])

48. What is the purpose of the activation function in neural networks?

Activation functions introduce non-linearity, allowing neural networks to learn complex patterns.

Why They Are Necessary

Without activation functions, a neural network behaves like a linear model, no matter how many layers it has.
Non-linearity helps the model learn curved boundaries, interactions, and complex features.

Common activation functions: ReLU, sigmoid, tanh, softmax, etc.

49. Compare and contrast different activation functions (ReLU, sigmoid, tanh).

Comparison Table

Optional Visualization Code

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-5, 5, 100)

plt.plot(x, 1/(1 + np.exp(-x)), label="Sigmoid")
plt.plot(x, np.tanh(x), label="Tanh")
plt.plot(x, np.maximum(0, x), label="ReLU")

plt.legend()
plt.title("Activation Functions")
plt.grid(True)
plt.show()

50. What is the vanishing gradient problem, and how is it addressed?

The vanishing gradient problem occurs when gradients become extremely small during backpropagation, slowing or stopping learning—common in deep networks.

Causes

Sigmoid/tanh saturate at large values → tiny gradients
Very deep architectures
Poor weight initialization

Solutions

Use ReLU or variants (Leaky ReLU, ELU)
Apply Batch Normalization
Use skip connections (ResNet)
Use He or Xavier initialization
Avoid excessively deep networks

Example Fix

# Instead of:
Dense(64, activation='sigmoid')

# Use:
Dense(64, activation='relu')

51️⃣ Difference Between Shallow vs Deep Neural Networks

Feature	Shallow NN	Deep NN
Hidden Layers	1–2	Many (10 to 100+)
Learning Ability	Simple patterns	Hierarchical complex features
Use Cases	Small datasets (Iris)	Images, NLP, voice
Training Time	Fast	Slow + compute heavy
Examples	Simple MLP	CNNs, RNNs, Transformers

Example:

Shallow NN: Can solve simple classification tasks.
Deep NN: ImageNet-level CNNs, GPT/Transformers.

52️⃣ Architecture of a CNN (Convolutional Neural Network)

A CNN processes image-like grid data using filters.

Standard CNN Flow

Input Layer → e.g., image (64×64×3)
Conv Layer → feature extraction
ReLU → non-linearity
MaxPooling → reduces size
Conv + Pool (repeat)
Flatten → convert to vector
Dense Layers → classification

Code Example (Keras)

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense

model = Sequential([
    Conv2D(32, (3, 3), activation='relu', input_shape=(64, 64, 3)),
    MaxPooling2D((2, 2)),
    Conv2D(64, (3, 3), activation='relu'),
    MaxPooling2D((2, 2)),
    Flatten(),
    Dense(64, activation='relu'),
    Dense(10, activation='softmax')
])

model.summary()

Output (Model Summary — simplified):

Layer (type)        Output Shape      Param #
------------------------------------------------
Conv2D              (None, 62,62,32)   896
MaxPooling2D        (None, 31,31,32)   0
Conv2D              (None, 29,29,64)   18496
MaxPooling2D        (None, 14,14,64)   0
Flatten             (None, 12544)      0
Dense               (None, 64)         803,840
Dense               (None, 10)         650
------------------------------------------------
Total params: ~824K

53️⃣ How RNNs Handle Sequential Data

RNNs are designed for time-dependent data such as text, speech, and time series.

Key Ideas

Maintain hidden state across time.
At each step:
hₜ = f(xₜ, hₜ₋₁)
Can capture short-term dependencies.

Limitations

Vanishing gradients → poor long-term memory.

Better Variants

LSTM → long-term memory via gates
GRU → simpler but effective gate design

Code Example (LSTM)

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Embedding, LSTM, Dense

model = Sequential([
    Embedding(input_dim=10000, output_dim=64),
    LSTM(128),
    Dense(1, activation='sigmoid')
])

model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])

Output (Model Summary — simplified):

Layer (type)      Output Shape       Param #
------------------------------------------------
Embedding         (None, None, 64)     640,000
LSTM              (None, 128)          98,816
Dense             (None, 1)            129
------------------------------------------------
Total params: ~739K

54️⃣ Role of the Embedding Layer in NLP

✔ Converts word IDs → dense vector representations

✔ Captures semantic meaning

✔ Reduces dimensionality vs one-hot encoding

✔ Enables relationships like:

king – man + woman ≈ queen

Popular Embeddings

Word2Vec
GloVe
fastText
BERT (contextual embeddings)

Code Example

from tensorflow.keras.layers import Embedding

embedding_layer = Embedding(
    input_dim=10000, 
    output_dim=64, 
    input_length=100
)

Output Shapes

Input: (batch_size, 100)
Output: (batch_size, 100, 64)

55️⃣ What is Transfer Learning?

Transfer Learning = Using a pre-trained model (trained on a huge dataset like ImageNet) and fine-tuning it for your own task.

How it Works

Load a pre-trained model
Freeze early layers (generic features like edges, textures)
Train top layers on your dataset (specific patterns)

Benefits

✔ Saves training time
✔ Works well even with small datasets
✔ Better generalization

56️⃣ What Are Pre-trained Models & How Are They Used?

Pre-trained models = Models already trained on large datasets (ImageNet, Wikipedia, COCO) that you can reuse.

Popular Pre-trained Models

Vision: VGG16, ResNet, EfficientNet, Inception
NLP: BERT, GPT, RoBERTa, DistilBERT

Use Cases

✔ Feature extraction
✔ Fine-tuning
✔ Transfer learning

Code Example — Using VGG16

from tensorflow.keras.applications import VGG16
from tensorflow.keras.models import Model
from tensorflow.keras.layers import GlobalAveragePooling2D, Dense

base_model = VGG16(weights='imagenet', include_top=False, input_shape=(224,224,3))

# Freeze base model
for layer in base_model.layers:
    layer.trainable = False

# Custom head
x = GlobalAveragePooling2D()(base_model.output)
x = Dense(1024, activation='relu')(x)
output = Dense(num_classes, activation='softmax')(x)

model = Model(inputs=base_model.input, outputs=output)

57️⃣ What is Backpropagation?

Backpropagation is the algorithm used to train neural networks by updating weights based on errors.

Steps

Forward Pass: Compute predictions
Loss Calculation: Compare with true label
Backward Pass: Compute gradients (using chain rule)
Weight Update: Apply gradient descent

Conceptually

Compute ∂L/∂w (sensitivity of loss to weight change)
Update:
w ← w − η × gradient

Where:

L = Loss
η = Learning rate
w = weights

58️⃣ SGD vs Batch Gradient Descent

Feature	Batch GD	Stochastic GD (SGD)
Data per update	Entire dataset	One sample
Speed	Slow	Fast
Stability	Stable, smooth	Noisy updates
Convergence	Exact minimum	Approximate
Memory	High	Low

Mini-Batch GD

➡ Uses small batches (e.g., 32, 64)
➡ Best of both worlds: faster + stable

59️⃣ How to Choose the Right Optimizer?

Optimizer	Description	Best For
SGD	Basic; stable	Small data, simple models
Adam	Adaptive LR + momentum	Most deep learning tasks
RMSProp	Good for non-stationary tasks	RNNs, time series
Adagrad	Large updates for rare features	NLP, embeddings
Adadelta	Fixes Adagrad’s decreasing LR	NLP

Code Example

from tensorflow.keras.optimizers import Adam, SGD

# Adam
optimizer = Adam(learning_rate=0.001)

# SGD + momentum
optimizer = SGD(learning_rate=0.01, momentum=0.9)

model.compile(optimizer=optimizer, loss='categorical_crossentropy')

60️⃣ Challenges in Training Deep Neural Networks

Challenge	Description	Solution
Vanishing/Exploding Gradients	Gradients shrink or blow up	ReLU, BatchNorm, Residual Blocks
Overfitting	Model memorizes data	Dropout, Early stopping, Regularization
Computational Cost	Too many params	GPUs, TPUs, distributed training
Data Scarcity	Deep nets need big datasets	Transfer learning, Data augmentation
Hyperparameter Tuning	Hard to find optimal settings	Grid search, Bayesian optimization

61️⃣ Difference Between Clustering & Classification

Feature	Clustering (Unsupervised)	Classification (Supervised)
Input	Only features (X)	Features + labels (X + y)
Goal	Discover hidden patterns/groups	Predict known class labels
Output	Cluster IDs	Class predictions
Examples	Customer segmentation	Spam detection

Examples

Clustering: Segment customers by purchase behavior
Classification: Predict whether an email is spam / not spam

62️⃣ Describe DBSCAN Algorithm

DBSCAN = Density-Based Spatial Clustering of Applications with Noise
Best for arbitrarily-shaped clusters & outliers detection.

Key Parameters

ε (epsilon): Neighborhood radius
MinPts: Minimum points to form a dense region

How It Works

A point is a core point if ≥ MinPts fall inside radius ε
Core points → connected into clusters
Non-reachable points → noise / outliers

Advantages

✔ Detects noise
✔ Works on arbitrary shapes
✔ No need to specify number of clusters

Code Example

from sklearn.cluster import DBSCAN
from sklearn.datasets import make_blobs

X, y = make_blobs(n_samples=300, centers=4, random_state=42)

dbscan = DBSCAN(eps=0.5, min_samples=5)
labels = dbscan.fit_predict(X)

63️⃣ How to Determine Optimal Number of Clusters in K-Means?

Methods

1. Elbow Method

Plot inertia vs k
Choose point where curve “bends”

2. Silhouette Score

Measures similarity within cluster vs nearest cluster
Higher = better

Elbow Method Code

from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

inertias = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(X)
    inertias.append(kmeans.inertia_)

plt.plot(range(1, 11), inertias, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Inertia')
plt.title('Elbow Method')
plt.show()

64️⃣ What is Silhouette Score?

Silhouette Score tells how well each point fits in its cluster.

Interpretation

Score	Meaning
+1	Perfectly clustered
0	On the cluster boundary
−1	Misclassified

Code Example

from sklearn.metrics import silhouette_score

kmeans = KMeans(n_clusters=4)
labels = kmeans.fit_predict(X)

score = silhouette_score(X, labels)
print("Silhouette Score:", score)

65️⃣ Explain Anomaly Detection

Anomaly detection identifies rare, unusual, or suspicious data points.

Use Cases

Fraud detection
Credit card scams
Cybersecurity
Manufacturing defects

Types

Method	Description
Supervised	Labeled normal + anomaly data
Semi-supervised	Train only on normal data
Unsupervised	No labels; detect points far from density

Approaches

Distance-based (KNN)
Density-based (DBSCAN, LOF)
Reconstruction error (Autoencoders)
Statistical (Z-score, Gaussian models)

✅ 66. How does the Isolation Forest algorithm work?

Isolation Forest is an anomaly detection method based on the idea that anomalies are easier to isolate than normal points.

Key Intuition

Anomalies = few & different → require fewer splits to isolate
Build many random isolation trees
Short average path length → anomaly
Long path length → normal point

Code Example

from sklearn.ensemble import IsolationForest

iso_forest = IsolationForest(contamination=0.1)  # Fraction of anomalies
iso_forest.fit(X)

anomalies = iso_forest.predict(X)  # -1 = anomaly, 1 = normal

✅ 67. What are Gaussian Mixture Models (GMMs)?

A Gaussian Mixture Model (GMM) assumes that the data is generated from a mixture of multiple Gaussian (normal) distributions.

Key Points

Each cluster = one Gaussian distribution
Performs soft clustering → each point gets a probability for each cluster
Uses Expectation-Maximization (EM) to find means, variances, and mixing weights

Code Example

from sklearn.mixture import GaussianMixture

gmm = GaussianMixture(n_components=4, random_state=42)
gmm.fit(X)

probs = gmm.predict_proba(X)  # Soft probabilities

✅ 68. Compare K-Means and GMMs

Feature	K-Means	GMM
Type	Hard clustering	Soft clustering
Cluster Shape	Spherical	Elliptical (more flexible)
Distribution Assumption	None	Gaussian distribution
Output	Single cluster label	Probability of belonging to each cluster
Sensitivity	Sensitive to centroid init	More robust
Complexity	Simple	More complex (covariance matrices)

Summary:

K-Means is simple & fast; GMM is more flexible & probabilistic.

✅ 69. What is the Expectation–Maximization (EM) algorithm?

EM is an iterative optimization algorithm used for models with latent (hidden) variables.

Two-Step Cycle

E-step:
Estimate expected log-likelihood using current parameters.
M-step:
Maximize this expected log-likelihood to update parameters.

Repeat until convergence.

Used in

Gaussian Mixture Models
Hidden Markov Models
Missing data imputation
Latent variable models

✅ 70. How do you evaluate the performance of clustering algorithms?

Clustering = unsupervised, so evaluation is tricky.

A) Internal Evaluation Metrics

(Do NOT require true labels)

1. Silhouette Score

Higher = better separation

2. Calinski–Harabasz Index

Higher = dense & well-separated clusters

3. Davies–Bouldin Index

Lower = better clusters

B) External Evaluation Metrics

(Require ground truth labels)

1. Adjusted Rand Index (ARI)

Measures similarity between cluster assignments and true labels
Range: [-1, 1]

2. Normalized Mutual Information (NMI)

Measures information shared between predicted and true labels
Range: [0, 1]

Code Example

from sklearn.metrics import adjusted_rand_score, normalized_mutual_info_score

true_labels = [0, 0, 1, 1, 2, 2]
predicted_labels = [1, 1, 0, 0, 2, 2]

ari = adjusted_rand_score(true_labels, predicted_labels)
nmi = normalized_mutual_info_score(true_labels, predicted_labels)

print("Adjusted Rand Index:", ari)
print("Normalized Mutual Info Score:", nmi)

✅ 71. What is a time series, and how is it different from other data types?

Time series: A sequence of data points recorded in chronological order.

Key Characteristics

Temporal ordering: Order of data points matters.
Autocorrelation: Current values often depend on past values.
Trend & Seasonality: Patterns over time (long-term trends, repeating cycles).

Comparison with other data types

Feature	Time Series	Cross-Sectional	Panel Data
Time Dependency	Yes	No	Partial (multiple entities over time)
Example	Stock prices over time	Customer age/gender	Sales across stores over time

✅ 72. Describe the components of a time series

Most time series can be decomposed into four main components:

Trend (T): Long-term upward or downward movement.
Seasonality (S): Repeating short-term cycles (daily, weekly, monthly).
Cyclical (C): Long-term fluctuations not of fixed period (e.g., business cycles).
Irregular / Noise (I): Random variation unexplained by other components.

Code Example

from statsmodels.tsa.seasonal import seasonal_decompose
import matplotlib.pyplot as plt

result = seasonal_decompose(data, model='multiplicative', period=12)
result.plot()
plt.show()

✅ 73. What is stationarity in time series data?

A time series is stationary if its statistical properties (mean, variance, autocorrelation) remain constant over time.

Why Stationarity Matters

Most classical forecasting models (ARIMA, etc.) assume stationarity.
Stationary series are easier to model and forecast accurately.

Types of Stationarity

Strict Stationarity: Full distribution invariant to time shifts.
Weak (Covariance) Stationarity: Mean, variance, and autocovariance are constant.

✅ 74. How do you test for stationarity?

1. Visual Inspection

Plot rolling mean & rolling standard deviation.
Look for trends or seasonality.

2. Statistical Tests

Augmented Dickey-Fuller (ADF) Test

Null hypothesis H0H_0H0: Unit root exists → non-stationary
Reject H0H_0H0 if p-value < 0.05 → stationary

Code Example

from statsmodels.tsa.stattools import adfuller

def adf_test(series):
    result = adfuller(series)
    print('ADF Statistic:', result[0])
    print('p-value:', result[1])
    print('Critical Values:')
    for key, value in result[4].items():
        print(f'   {key}: {value}')

adf_test(data)

✅ 75. Explain the Autoregressive Integrated Moving Average (ARIMA) model

ARIMA(p, d, q) is a widely used model for univariate time series forecasting.

Parameters

p: Number of autoregressive terms (AR) – depends on past values.
d: Degree of differencing to make series stationary (I).
q: Number of moving average terms (MA) – depends on past forecast errors.

How It Works

AR(p): Predicts using past values.
I(d): Differencing removes trend/seasonality.
MA(q): Predicts using past errors.

Code Example

from statsmodels.tsa.arima.model import ARIMA

model = ARIMA(train_data, order=(1,1,1))  # ARIMA(1,1,1)
results = model.fit()
forecast = results.forecast(steps=10)

✅ 76. Difference between AR, MA, and ARIMA models

Model	Description	Use Case
AR(p)	Autoregressive model; predicts current value using past values.	When current values depend on their own history.
MA(q)	Moving Average model; predicts current value using past forecast errors.	When current value depends on errors of previous predictions.
ARIMA(p,d,q)	Combines AR + I (integration/differencing) + MA.	For non-stationary time series where differencing is needed.

✅ 77. Handling seasonality in time series data

Approaches:

Seasonal Decomposition: Remove seasonal component to analyze trend & residuals.
Seasonal Differencing: Subtract value from previous season (e.g., y_t - y_{t-12} for monthly data).
Seasonal Models: Use models like SARIMA:
- SARIMA(p,d,q)(P,D,Q)m
- m = number of periods per season (e.g., 12 for monthly data)

Code Example (SARIMA)

from statsmodels.tsa.statespace.sarimax import SARIMAX

# SARIMA(1,1,1)(1,1,1,12)
model = SARIMAX(data, order=(1,1,1), seasonal_order=(1,1,1,12))
results = model.fit()
forecast = results.get_forecast(steps=12)

✅ 78. Exponential Smoothing

Exponential smoothing assigns decreasing weights to older observations.

Types

Simple Exponential Smoothing (SES): Captures level only.
Holt’s Linear Trend Method: Level + trend.
Holt-Winters Method: Level + trend + seasonality.

Code Example (Holt-Winters)

from statsmodels.tsa.holtwinters import ExponentialSmoothing

model = ExponentialSmoothing(data, trend='multiplicative', 
                             seasonal='multiplicative', seasonal_periods=12)
fit = model.fit()
forecast = fit.forecast(steps=12)

✅ 79. Lag in time series analysis

Lag: Shifting the time series by one or more periods.
Lag-1: Uses value at t-1 to predict value at t.
Uses:
- Autocorrelation analysis
- Feature engineering for models like LSTMs or AR models

Code Example (Create Lag Features)

data['lag1'] = data['value'].shift(1)
data['lag2'] = data['value'].shift(2)
print(data[['value', 'lag1', 'lag2']].head())

✅ 80. Evaluating accuracy of time series forecasts

Code Example

from sklearn.metrics import mean_absolute_error, mean_squared_error
import numpy as np

mae = mean_absolute_error(test, forecast)
mse = mean_squared_error(test, forecast)
rmse = mean_squared_error(test, forecast, squared=False)
mape = np.mean(np.abs((test - forecast) / test)) * 100

print(f"MAE: {mae}, MSE: {mse}, RMSE: {rmse}, MAPE: {mape:.2f}%")

✅ 81. What is Reinforcement Learning (RL)?

Definition:
Reinforcement Learning is a type of machine learning where an agent learns by interacting with an environment, taking actions to maximize cumulative reward over time.

Key Components

Component	Description
Agent	The learner or decision-maker that performs actions.
Environment	The world or system the agent interacts with.
State (s)	Representation of the current situation in the environment.
Action (a)	Choices the agent can make at each state.
Reward (r)	Feedback received after taking an action; guides learning.
Policy (π)	Strategy that maps states to actions.
Value Function (V(s))	Expected cumulative reward from a given state.
Q-Function (Q(s,a))	Expected cumulative reward from a state-action pair.

How RL Works

Agent observes the current state of the environment.
Agent chooses an action based on its policy.
Environment returns a reward and updates to a new state.
Agent updates its policy/value function to improve future decisions.
Repeat until the agent learns an optimal strategy.

Example Use Cases

Games: AlphaGo, Chess, Atari games
Robotics: Teaching robots to walk or pick objects
Finance: Portfolio management, trading strategies
Recommendation Systems: Personalized content selection

82. Exploration vs. Exploitation Dilemma

In RL, the agent must balance between:

Strategy	Description
Exploration	Try new actions to discover potentially better rewards.
Exploitation	Use known actions that currently yield the highest reward.

Why it matters:

Pure exploitation may miss better rewards.
Pure exploration wastes time on suboptimal actions.

Common Strategies to Balance:

ε-greedy:
- With probability ε, choose a random action (explore).
- With probability 1-ε, choose the best-known action (exploit).
Softmax (Boltzmann Exploration):
- Select actions probabilistically based on estimated Q-values.
Upper Confidence Bound (UCB):
- Chooses actions with the highest upper bound of expected reward, balancing uncertainty.

83. Markov Decision Processes (MDPs)

Definition:
MDPs are a mathematical framework for modeling sequential decision-making where outcomes are partly random and partly under control.

Components:

Component	Description
States (S)	All possible situations the agent can be in.
Actions (A)	Choices available to the agent.
**Transition Model P(s’	s, a)**
Reward Function R(s, a, s’)	Immediate reward received after taking action a in state s and transitioning to s’.
Discount Factor γ	Weight for future rewards (0 ≤ γ ≤ 1).

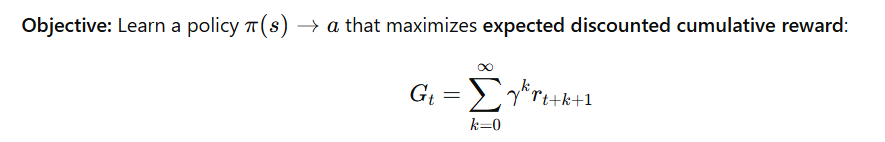
84. Q-Learning

Definition:
Q-learning is a model-free, off-policy RL algorithm that learns the optimal action-value function Q(s,a)Q(s, a)Q(s,a) without needing a model of the environment.

How it works:

Python Example (FrozenLake):

import gym
import numpy as np

env = gym.make('FrozenLake-v1')
q_table = np.zeros([env.observation_space.n, env.action_space.n])

alpha = 0.8   # learning rate
gamma = 0.95  # discount factor
episodes = 2000

for _ in range(episodes):
    state = env.reset()
    done = False
    while not done:
        action = np.argmax(q_table[state])
        next_state, reward, done, info = env.step(action)
        q_table[state, action] += alpha * (reward + gamma * np.max(q_table[next_state]) - q_table[state, action])
        state = next_state

Notes:

Off-policy means Q-learning learns the optimal policy independently of the agent’s actions.
Converges to the optimal Q-values over time.

85. Role of the Reward Function in Reinforcement Learning

The reward function defines the agent’s objective by assigning feedback for each action in a given state. It essentially tells the agent what is “good” or “bad.”

Key Points:

Guides the agent’s behavior toward desired goals.
Must be informative, but not too sparse.
Poorly designed rewards can lead to unintended behaviors.

Examples:

Game: +1 for winning, -1 for losing, 0 otherwise.
Robotics: Reward smooth movement, penalize energy use.

86. Policy Gradients

Policy gradient methods directly optimize the policy πθ(a∣s)\pi_\theta(a|s)πθ(a∣s) instead of estimating Q-values.

How it works:

Advantages:

Works with continuous action spaces.
Stochastic policies allow natural exploration.

Disadvantages:

High variance in updates.
Sample inefficient.

Popular Algorithms:

REINFORCE
Actor-Critic
A2C (Advantage Actor-Critic)

87. Model-Based vs Model-Free RL

Feature	Model-Based RL	Model-Free RL
Environment Model	Needs transition & reward model	Learns directly from experience
Planning	Can plan ahead using the model	No planning, learns policy/value directly
Efficiency	More sample-efficient	Less sample-efficient
Complexity	Harder to build accurate models	Simpler to implement
Examples	Dyna, PILCO	Q-learning, SARSA, DQN

88. GAN Architecture

Generative Adversarial Networks consist of two networks competing:

Generator (G): Creates fake data from random noise.
Discriminator (D): Classifies real vs generated data.

Training Process:

G tries to fool D by generating realistic samples.
D tries to distinguish real from fake.
Training continues until a Nash equilibrium is reached.

89. GANs vs Autoencoders

Feature	GANs	Autoencoders
Goal	Generate realistic samples	Reconstruct input data
Architecture	Two competing networks	Encoder-decoder structure
Latent Space	Random noise (non-interpretable)	Encoded representation
Training	Adversarial (game-theoretic)	Minimize reconstruction loss
Output Quality	Often sharp and realistic	May be blurry
Stability	Hard to train, mode collapse issues	Generally stable

90. Challenges in Training GANs

Common Challenges:

Mode Collapse: Generator produces limited variety.
Instability: Training oscillates or diverges.
Vanishing Gradients: Discriminator becomes too strong.
Evaluation Difficulty: No single metric for quality/diversity.
Hyperparameter Sensitivity: Small changes can break training.

Solutions:

Use Wasserstein GAN (WGAN) or WGAN-GP.
Add gradient penalty.
Alternate training of D and G.
Apply spectral normalization.
Monitor metrics like FID score.

91. How to Deploy a Machine Learning Model

Deploying a model moves it from development to production so it can make real-time predictions.

Key Steps:

Model Training & Evaluation
- Train and validate the model locally using historical data.
- Ensure metrics meet business requirements.
Model Serialization
- Save the trained model for reuse.
- Common formats:
  - pickle / joblib (Python)
  - ONNX (cross-platform)
import joblib # Save trained model joblib.dump(model, 'model.pkl') # Load model in production loaded_model = joblib.load('model.pkl')
API Development
- Wrap the model in a REST or gRPC API.
- Use frameworks like Flask, FastAPI, or Django.
Containerization
- Package the model and API in Docker for consistent environments.
Cloud Hosting
- Deploy to platforms like AWS (SageMaker, EC2), GCP (AI Platform), Azure, or Heroku.
Monitoring & Logging
- Track model performance, latency, and errors in real-time.

92. Common Challenges in Model Deployment

Challenge	Description
Scalability	Efficiently handle high volumes of requests.
Latency	Ensure fast inference for real-time applications.
Versioning	Manage multiple versions of models and APIs.
Data Drift	Input data may change over time, reducing accuracy.
Security	Protect against adversarial attacks and unauthorized access.
Integration	Ensure compatibility with existing systems, databases, and pipelines.

93. Monitoring Deployed Models

Monitoring ensures that models remain reliable and effective after deployment.

Key Metrics:

Accuracy or other performance metrics over time.
Prediction latency (speed of inference).
Input data distribution shifts (detect data drift).
Error rates or failed predictions.
Confidence scores of predictions.

Tools:

Prometheus + Grafana: Metrics collection and visualization.
MLflow: Logging and model versioning.
AWS CloudWatch: Monitoring on AWS.
Azure Application Insights: Monitoring on Azure.

Example – Logging Predictions:

import logging
logging.basicConfig(filename='model_logs.log', level=logging.INFO)

def predict(input_data):
    prediction = model.predict(input_data)
    logging.info(f"Input: {input_data}, Prediction: {prediction}")
    return prediction

94. What is Model Drift, and How Do You Detect It?

Definition:
Model drift occurs when the statistical properties of input data or the relationship between input and output change over time, leading to degraded model performance.

Types of Drift:

Concept Drift: Relationship between features and target changes.
- Example: Customer behavior changes over time.
Data Drift: Input feature distribution changes.
- Example: Sensor readings gradually shift due to hardware aging.

Detection Methods:

Statistical Tests:
- Kolmogorov-Smirnov (KS) Test, Chi-square test, etc.
Monitoring Tools:
- Evidently AI, NannyML, WhyLogs.
Performance Drop:
- Compare model performance metrics (accuracy, RMSE) over time against baseline.

Code Example (KS Test for Data Drift):

from scipy.stats import ks_2samp

# Compare train vs new data feature distributions
stat, p_value = ks_2samp(X_train['feature'], X_new['feature'])

if p_value < 0.05:
    print("Drift detected!")
else:
    print("No significant drift.")

95. How to Handle Real-Time Predictions

Real-time prediction systems must deliver low-latency responses for incoming requests.

Best Practices:

Use lightweight or optimized models (LightGBM, small neural networks).
Cache frequent responses to reduce computation.
Use asynchronous processing for batch or queued inference.
Optimize model inference using frameworks like ONNX, TensorRT, or TensorFlow Lite.

Code Example (FastAPI Real-Time Inference):

from fastapi import FastAPI
import joblib

app = FastAPI()
model = joblib.load("model.pkl")

@app.post("/predict")
def predict(data: dict):
    prediction = model.predict([data["features"]])
    return {"prediction": prediction.tolist()}

96. Role of APIs in Model Deployment

Definition:
APIs (Application Programming Interfaces) act as an interface for external applications to interact with your deployed model.

Benefits:

Decouples model logic from application logic.
Enables scalability and load balancing via RESTful or gRPC interfaces.
Facilitates integration with mobile apps, web apps, dashboards, or other services.

Common Frameworks:

Flask: Lightweight, simple to use.
FastAPI: Fast, supports asynchronous requests.
Tornado / Django REST Framework: Useful for high-performance or complex applications.

97. Ensuring Data Privacy and Security in ML Applications

Privacy Considerations:

Data Anonymization: Remove personally identifiable information (PII) before training.
Encryption: Use HTTPS/TLS for data in transit; encrypt stored data.
Access Control: Role-based access, authentication, and audit logs.
Compliance: Follow regulations like GDPR, HIPAA, CCPA.

Techniques:

Federated Learning: Train models across decentralized data sources without sharing raw data.
Differential Privacy: Add noise to data or gradients to prevent leakage of individual records.
Secure Multi-party Computation: Joint computations without revealing private data.

Tools:

IBM AI Fairness 360
Google Differential Privacy Library
TFX (TensorFlow Extended) for secure and reproducible pipelines

98. Ethical Considerations in Machine Learning

Key Issues:

Bias & Discrimination: Models can reflect historical or dataset biases.
Transparency: Black-box models can be hard to interpret.
Accountability: Determining responsibility for harmful decisions.
Surveillance & Consent: Avoid using personal data without consent.
Environmental Impact: Large models consume significant compute and energy.

Frameworks & Initiatives:

FAT Conference:* Fairness, Accountability, Transparency
Partnership on AI
Microsoft Fairlearn: Tools to assess fairness

99. Handling Bias in ML Models

Strategies:

Audit Data: Check distributions across sensitive attributes (e.g., gender, race).
Fairness Metrics: Use metrics like disparate impact or equal opportunity difference.
Bias Mitigation Techniques:
- Reweighting: Adjust weights of samples during training.
- Adversarial Debiasing: Train models to minimize bias signal.
- Post-processing Calibration: Adjust predictions to improve fairness.

Code Example (Fairlearn):

from fairlearn.metrics import MetricFrame
from sklearn.metrics import accuracy_score

metric_frame = MetricFrame(
    metric=accuracy_score,
    y_true=y_test,
    y_pred=predictions,
    sensitive_features=sensitive_attr
)

print(metric_frame.overall)
print(metric_frame.by_group)

100. Best Practices for Maintaining and Updating Deployed Models

Key Practices:

Continuous Monitoring: Track model performance and detect data drift.
Retraining Pipelines: Automate retraining with new or fresh data.
Version Control: Use DVC, MLflow, or Git to track model versions.
Rollback Strategy: Keep older versions for fallback in case of failure.
A/B Testing: Safely test new models in production with a subset of traffic.
Documentation: Maintain logs, model metadata, and retraining history.

Code Example (Automated Retraining Trigger):

from datetime import datetime

last_retrain_date = datetime(2024, 1, 1)

if (datetime.now() - last_retrain_date).days > 30:
    print("Triggering retraining...")
    # Call retraining function here